CS301 HW13
May 2021
代写计算机理论作业 HITTING SET = < S, T, h > S is a set, T is a set of subsets of S, and h is an integer where there is S’ S with S’ = h and S’ contains at least one element
Part One 代写计算机理论作业
Answer the following questions regarding HIT- TING SET and VERTEX COVER as defined be- low.
HITTING SET = < S, T, h > S is a set, T is a set of subsets of S, and h is an integer where there is S’ S with S‘ = h and S‘ contains at least one element from each set in T} VERTEX COVER = < tt, k > tt = (V, E) is an undirected graph that con- tains a set of k nodes that touch all edges in G}
a.Find a hitting set S’ of size h=2 for the sets S = {a, b, c, d, e, f, g}and T = {{a, b, c , c, d, e , e, f, g}}.
Solution
Given the defifinition of HITTING SET, we can let S0 = {c, e}. Then for each set in T, S’ contains at least one element in this set:
c ∈ {a, b, c}
c ∈ {c, d, e}
e ∈ {e, f, g}
|S‘ | = 2
b.Find a vertex cover of size 2 for the graph G = (V, E) where V ={a, b, c, d, e} and E = {{a, b}, {b, c}, {a, d}, {b, e}, {d, e}}.
Solution
From the defifinition of VERTEX COVER, we can let the vertex cover of G to be {b, d}. Therefore all edges were touched by either node in the vertex cover.
c.Describethe certificate for a polynomial time verifier for VERTEX _COVER.

Solution 代写计算机理论作业
The certifificate for the verififier of VERTEX COVER problem is the set of nodes with at most k elements.
The verififier for VERTEX COVER is that:
V = On input << G, k >, c >:
1.Test if c is a set with k nodes, and all of them are in graph G.
2.Test if for every edge in G, either ends of the edge is in the set c.
d.Describethe certificate for a polynomial time verifier for HITTING_SET.
Solution 代写计算机理论作业
The certifificate for HITTING SET is a set of k elements from the original
set S, or namely the set S’. With this certifificate, the verififier for HITTING SET
is that:
V = On input << S, T, h >, S0 >:
1.Test if S’ is a subset of S, or that every element in S’ is in S.
2.Test if for every set in T, there is at least one element of this set in S’.
e.Describe a polynomial time reduction from VERTEX COVER to HIT- TING
Solution Note that both certifificates of the two problem are sets, we can
reduce the problem of VERTEX COVER to HITTING SET using the following
function:
f(edge in E) = {a, b}
where a, b are the both ends of the edge. Therefore we can let f(E) ={{ae, be}}for all e in E}. And then we can use the verififier of HITTING SET to verify the problem of VERTEX COVER.
2 Use the reductions described in the book to perform the following conversions. 代写计算机理论作业
2a
Φ = (a ∨ b) ∧ (a ∨ ¯b ∨ c ∨ d)
Solution
The SAT in CNF form can be converted to 3-SAT:
Φ = (a ∨ b) ∧ (a ∨ ¯b ∨ c ∨ d)
= (a ∨ b ∨ y) ∧ (a ∨ b ∨ y’ ) ∧ (a ∨ ¯b ∨ z) ∧ (z‘ ∨ c ∨ d)
Now the the CNF is converted into 3-SAT
2b
Φ = (a ∨ b ∨ b) ∧ (a¯ ∨ ¯b ∨ ¯b)
Solution 代写计算机理论作业
The reduction described in the book would turn the 3SAT problem into a
CLIQUE problem by constructing the graph below:
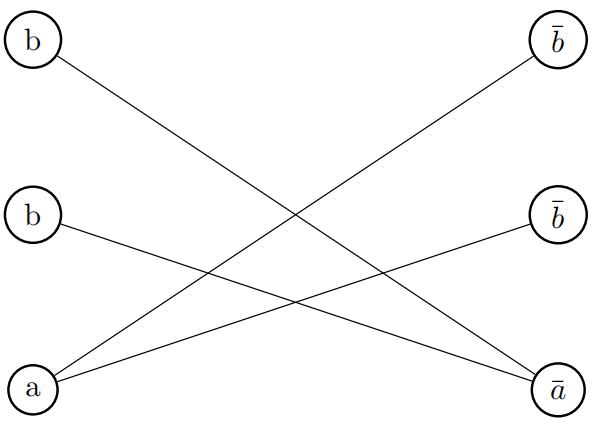
2c
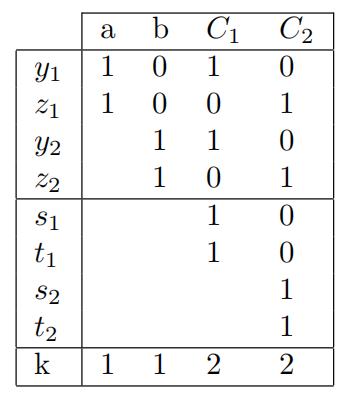
Φ = (a ∨ b ∨ b) ∧ (a¯ ∨ ¯b ∨ ¯b)
Using the algorithm to convert the 3SAT to SUBSET-SUM, we will have the following representation described in the table for the clauses (0 in the table was ignored for simplicity)

更多代写:应用经济学网课代修 多邻国代考 哲学网课代修推荐 宗教paper代写 英国项目管理硕士毕业论文代写 论文代写机构价格
