编程作业代写价格 At each of the 12 positions you plan to build one building that is either a quarry, or a factory, or a market.There are three types
Programming Assignment
Due date: Friday, December 10th, 2021, noon, via SAM (https://sam.csc.liv.ac.uk/COMP/Submissions.pl?strModule=COMP331 or https://sam.csc.liv.ac.uk/COMP/Submissions.pl?strModule=COMP557)
This assignment is worth 15% of your grade. 编程作业代写价格
The following graph shows 12 positions with connections (this arrangement is called the Frucht graph1):
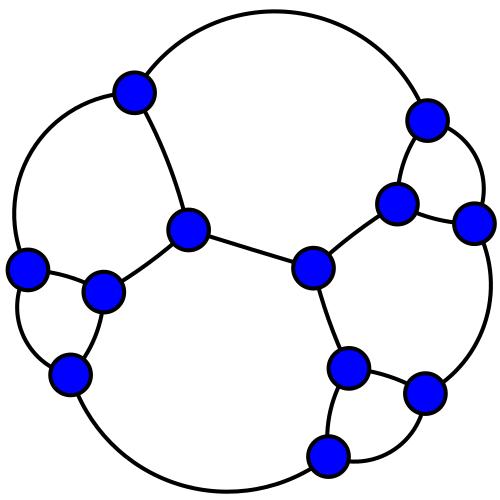
At each of the 12 positions you plan to build one building that is either a quarry, or a factory, or a market.
There are three types of resources: gold, diamonds, and jewellery. Every year the same amount of resources are being sent from building to building over the connections. There is a limitation though for each connection: In every year the sum of all resources that are being sent over a connection cannot exceed 165 units in total (for example, if 100 units of gold are being sent from a to b, then the amount of diamonds that are being sent from b to a is at most 65).

Every year you have 850 units of energy available. Energy is not transported through the network, but is available everywhere. 编程作业代写价格
- Every year a quarry produces 200 units of gold and 75 units of diamonds. This costs 100 units of energy.
- Every year a factory uses 70 units of gold and 20 units of diamonds and produces 60 units of This costs 300 units of energy.
- The market sells gold, diamonds, and jewellery. 编程作业代写价格
- A unit of gold gives£150.
- Aunit of diamonds gives £200.
- A unit of jewellery gives£1000.
Selling costs no energy. The sum of all revenues of all markets is called the total revenue.
Resources cannot be carried over between years. Quarries and factories are not required to use up all resources. You can decide to forward or destroy an arbitrary amount of resources. The forwarding and the destruction of resources cost no energy. You also do not have to sell everything that gets sent to a market. You can forward those resources instead. It obviously makes no sense to forward jewellery through a market instead of selling it, but it could in principle be useful to forward gold or diamonds instead of selling them, so that they can be converted to jewellery at a factory.
Quarries and factories can run on an efficieny lower than 100%. Their input, their output, and their energy usage scale down linearly.
On the next page is a graphical presentation of an optimal solution for a specific fixed arrangement of buildings. Quarries are yellow, factories are blue, and markets are red. G stands for gold, D stands for diamond, J stands for jewellery. The efficiencies are shown within the circles.
1https://en.wikipedia.org/wiki/Frucht_graph
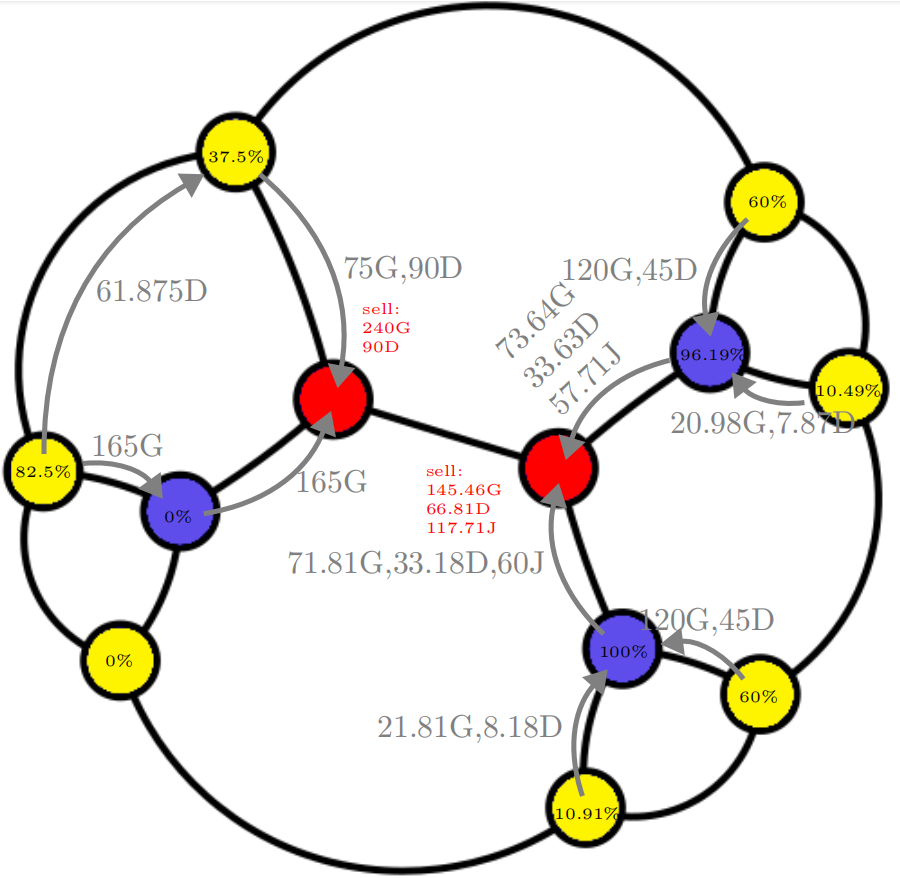
In principle it is possible to send resources in opposing directions at the same time over a connection, but this example makes no use of that. The energy consumption in this example is (82.5% + 37.5% + 60% + 10.40% +60% + 10.91%) · 100 + (100% + 96.19%) · 300, which (with more decimal digits) is exactly 850. The total revenuein this example is (with more decimal digits than in the figure) £(240 + 145.468) · 150 + £(66.8129 + 90) · 200 +£117.719 · 1000, which (with more decimal digits) is £206902.0468.
Your task is to place the buildings, set the efficiencies, and route the resources so that the total revenue is maximised.
- Writea program P1 in a programming language of your choice that creates an .lp file and then calls glpsol to solve the task for a fixed placement of buildings.
- Since for every location there are three possible buildings, there are 312= 531 441 many placements of buildings in total. Write a program P2 that calls your program P1 on each placement and selects the optimal My old laptop can solve 1000 such LPs in roughly 5 seconds, so this computation takes less than one hour. 编程作业代写价格
- Takethe optimal solution (or one of the optimal solutions, if several are optimal) and draw a corresponding figure analogously to the example figure on this page and put it into a .pdf file.
Submission format: Put the following into a single .zip file:
- Your program code.
- One of the 531 441 many .lp files that was generated by P1and that gives the optimal objective function value.
- The .pdf file containing the figure of the optimal solution.
If you have trouble with the programming, please try get help from your tutor or your lecturer. Do not copy another student’s solution!
Only for COMP557, not for COMP331 – research component
Additionally, modify this assignment several times and observe how the optimal solutions change. Then formu- late a hypothesis and verify or falsify it with further tests. Write down what you have done. This should be no longer than one A4 page. Add this page to the submission .zip file.

更多代写:留学生网课代包 多邻国代考 留学生微积分Final exam代考 留学生英文求职信代写 留学生英文论文写作 英国硕士论文查重率

