优化考试代考 Optimization代写

Optimization

Finance and Accounting, Management, Marketing Management

Exam Total Time: 2h15 (plus 15min of tolerance)

优化考试代考 Part 1 In the questions of Part 1 you should present only your answer, and should not show any calculations or justifications.

Important observations: 优化考试代考

The use of calculators is not allowed and all electronic devices must be turned off for the whole duration of the test.
The use of course materials or any other consultation materials is not allowed.
All replies must be properly justified and written on the sheets provided, and the staple must not be removed. Red ink and pencils are not allowed.
The last sheet may be used for auxiliary computations, or, exceptionally, to answer questions, if extra space is needed.
No questions will be answered.

Part 1 优化考试代考

In the questions of Part 1 you should present only your answer, and should not show any calculations or justifications.

1.

Let A, B, C and D be matrices with real entries such that:

A ∈ M₃_×₃and |A| = 4;
B is a matrix in the row echelon form that is obtained from A by applying the following sequence of elementary row operations:

R₁ ↔ R₂ ; R₁ → 1/2R₁ ; R₃ → R₃ − 3R₂

C is the matrix corresponding to the quadratic form Q(x, y, z) = x²− y²− z² + 2yz;
D = [1 0 0]^T.

One can say that:

(a) The size of the matrix 2D^T(C + B)A⁻¹ is _________ .

(b) The matrix C is symmetric/invertible (cross out what doesn’t matter) and is given by

(d) The quadratic form Q(x, y, z) corresponding to C is (cross out what doesn’t matter):

positive semi-definite / negative semi-definite / indefinite.

(e) Regarding the existence of system solution, the linear system AX = D is (cross out what doesn’t matter):

consistent and independent / consistent and dependent / inconsistent.

2.

Let f : R²→ R be a differentiable function and let (a, b) be a critical point of f. Suppose that f(a, b) = 1, f_xx(a, b) = 5, f_xy(a, b) = f_yx(a, b) = 2 and f_yy(a, b) = 1.

(b) In relation to the function f, the point (a, b) is a (cross out what doesn’t matter):

local maximum point / local minimum point / saddle point.

Part 2 优化考试代考

In the questions of Part 2 you should present your reasoning clearly, indicating all necessary calculations and justifications.

1.

Consider the linear system with unknowns x, y and z,

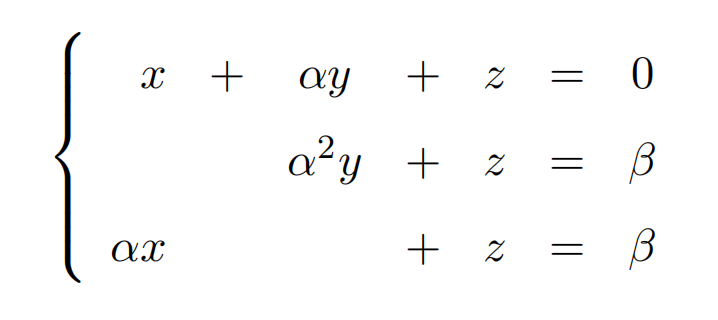
where α and β are real parameters.

(a) Write the given system in the matrix equation form AX = B, where X = [x y z]^T is a column-vector containing the unknowns.

(b) Using Gaussian elimination, classify the system as a function of the real parameters α and β.

(d) If we look at the parameter β as an additional unknown, we still obtain a linear system. Represent such system in the matrix equation form CY = D, where Y = [x y z β]^T , that is, determine the rectangular matrix C and the column-vector D.

2.

Let A be a 3 × 3 matrix such that:

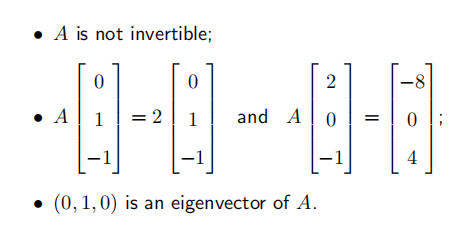
(a) What is the value of det(A + 4I₃)? Justify.

(b) Justify that λ = 0 is an eigenvalue of A and (0, 1, 0) is a corresponding eigenvector.

(d) Find an invertible matrix P ∈ M₃_×₃ and a diagonal matrix D ∈ M₃_×₃ such that D = P⁻¹AP.

(e) Without performing any calculation, explain how to use the matrices P and D from the previous paragraph to compute the power matrix A⁵.

3.

Let A be an invertible matrix of size n × n and let λ be an eigenvalue of A and v a corresponding eigenvector.

(a) Prove that λ is also an eigenvalue of A^T .

(b) Prove that v is also an eigenvector of A⁻¹ and indicate the corresponding eigenvalue.

4.

Consider the real function of two real variables

f(x, y) = x³ − 3xy² + 6x² − 6y² + 2

(a) Find the critical points of f and classify them.

(b) Determine an equation of the tangent plane to the graph surface of f at the point (1, 1, 0).

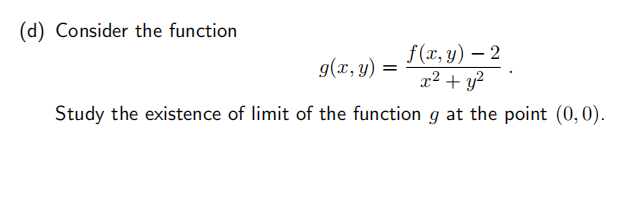
5.

Consider the function f(x, y) = x²− y².

(a) Justify that f has absolute extrema when subject to the condition x² + y² = 1.

(b) Using Lagrange Multipliers Method, determine the values of the absolute extrema of f subject to x² + y² = 1.

合作平台：essay代写论文代写写手招聘英国留学生代写