MT4512 Automata, Langugages and Complexity
Class Test
数学测试代写 This class test forms 10% of the assessment for this module. It will be marked out of 20 marks. Please answer all five questions,
This class test forms 10% of the assessment for this module. It will be marked out of 20 marks.
Please answer all five questions, fully justifying your answers. You may cite results from the course without proof, but you must state the name or number of the result you are using.
1. 数学测试代写
Let G1be the context free grammar (S, {0, 1}, S → 0S |S1 | 0 | 1, S).
(a) For each of the following two words, either give a derivation or prove that it is not in L(G1): 021, 10. [2 marks]
(b) Describe L(G1) and fully justify your answer. [3 marks]
(c) Construct a PDA P s.t. L(P) = L(G1). [2 marks]
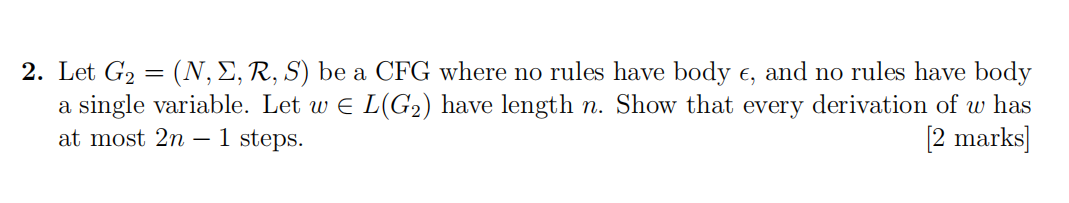
3.
Let L1= {(ab)ncnan: n ≥ 0}. Prove that L1 is not context free. [3 marks]
4. 数学测试代写
Let L2 be the language
{0a1b#0a+b : a, b ∈Z≥0}
over the alphabet {0, 1, #}. Give an implementation-level description of a Turing machine M to recognise L2. [4 marks]
5. 数学测试代写
Let M1and M2 be Turing machines, and let L3= L(M1) and L4 = L(M2).
(a) Prove that L3 ∪ L4 is Turing recognisable. [2 marks]
(b) If both M1 and M2 are deciders, is L3 ∩ L4 decidable? Justify your answer. [2 marks]

更多代写:计算机网课Online Course代上代修 GRE代考 英国统计学作业Assignment代写 审计学代写essay案例 商业计划书北美代写 代写机构推荐
