Multivariate Calculus
多元微积分代写 EXAM DURATION: 2 hours EXAM INSTRUCTIONS: Attempt ALL questions. The number in square brackets shows the maximum marks obtainable for
EXAM DURATION: 2 hours
EXAM INSTRUCTIONS: Attempt ALL questions.
The number in square brackets shows the maximum marks obtainable for that question or part-question.
Your answers should contain the full working required to justify your solutions.
INSTRUCTIONS FOR ONLINE EXAMS:
Each page of your solution must have the page number, module code, and your student ID number at the top of the page. You must make sure all pages of your solutions are clearly legible.
1.

(a) Calculate the directional derivative of f in the direction of the line. [4]
(b) Hence, identify the point where f takes its maximum value along the line. [2]
2.
Determine the two points on the surface
f(x, y, z) = x2 − 2y2 − 4z2 + xy + xz = 12 ,
at which the tangent plane to f is parallel to the plane
12x − 2y + 22z = 5 . [8]
3. 多元微积分代写
Using the Method of Lagrange Multipliers, determine the point on the plane
2x + 3y + 4z = 11 ,
such that the function f = 4x2 + y2 + 5z2 has its minimum value. [8]
4.
(a) State the conditions that stationary points of a general function f(x,y) have to satisfy to be classified as (i) maxima, (ii) minima or (iii) saddle points. Define all the terms you use. [2]
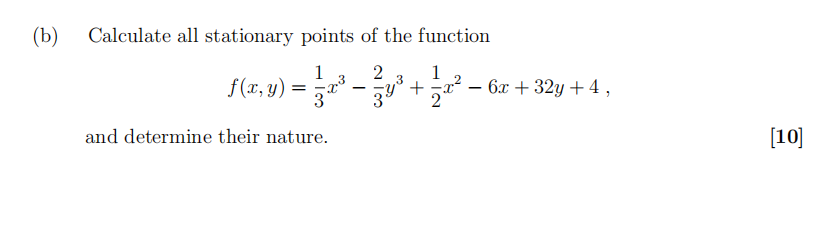
5. 多元微积分代写
Evaluate the integral
∫∫A cos(x2 + y2) dA
where A is the portion of {(x, y) : a2 ≤ x2 +y2 ≤ b2 } for which x ≥ 0. What is the limit of the result as a → 0 and b → √π [6]
6. 多元微积分代写
Some damp sand is piled into the shape of a paraboloid defifined as the region V enclosed by the surface az = a2 − x2 − y2 and the base z = 0. The water content of the sand is given by
ρ(x, y, z) = k(a2 − x2 − y2 − az)
where k is a constant.
The mass of water in the sand is given by
∫∫∫V ρ(x, y, z) dxdydz.
Use cylindrical polars to calculate the total water content in V . [6]
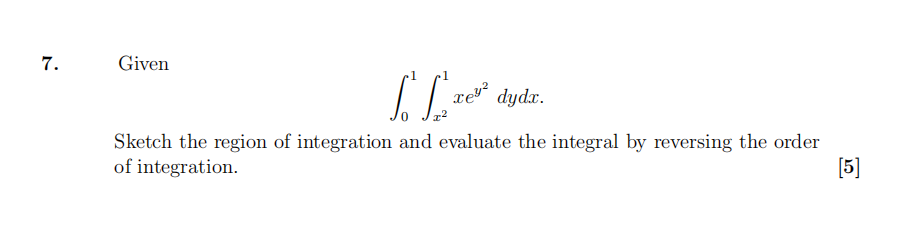
8.
Find the volume bounded by the vertical surface y = x2 and by the planes
2x + y + z = 3 and z = 0. [10]
9. 多元微积分代写
Let V be the portion of a sphere of radius a centred at the origin for which
x, y ≥ 0. Evaluate
∫∫∫V x2 dV. [9]

更多代写:计算机留学生Coursework代写 GRE代考 英国历史assignment代写 留学Essay代写推荐 留学论文分析代写 代修数学网课
