Econ 390, Fall 2019, Midterm Exam I: Solution
新西兰经济代考 About 97% of total variation of the actual exchange rate is explained by (the variation of ) this predicted exchange rate.
Question 1: 新西兰经济代考
(20=4*5 pts) TRUE/FALSE. State if the following statements are true or false. Only clearly and correctly explained answers will earn full credit.
(a)The sample correlation of the OLS residuals with explanatory variable is positive or negativedependent on whether the explanatory variable is mostly positive or negative.
FALSE: Sample average of OLS residuals is zero (this is one of the two first-order con- ditions for OLS estimator).
(b)R2is a measure of how close the values of the dependent variable yi are to the estimated regression line: a larger value of R2 indicates that the yi’s are closer to that line.
TRUE: the closer yi’s are to the regression line (i.e., to yˆi’s), the smaller is the SSR. Since SST = SSE + SSR, the smaller is SSR, the larger is SSE, and consequently, R2.
(c)Thefollowing linear regression model that explains CEO annual salary (salary, in
$1,000) in terms of annual firm sales (sales, in $1,000) was estimated:
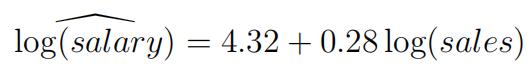
FALSE: This is a log-log model, so the slope coefficient is interpreted as elasticity: keeping other things fixed, a 1% increase in sales is associated with a 0.28% increase in salary.
(d)Inthe following model, the slope coefficient for log(sales) is not statistically significant at the 1% level.
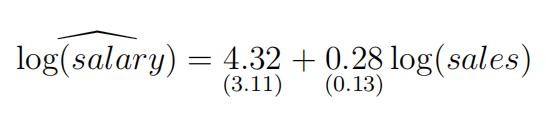
TRUE: t = 0.28 = 2.15 < 2.575 (the 1% two-sided critical value), so it’s not significant at the 1% level.
Question 2:
(15 pts) Below you are asked to decide on whether or not to use a one-sided alternative or a two-sided alternative hypothesis for the slope coefficient. Briefly justify your decision and state the corresponding null and alternative hypotheses in terms of model’s parameter(s).
(i)Model:
CourseEval = β0 + β1OneCredit + u,
where CourseEval is course overall teaching evaluation score, and OneCreidt is a dummy variable equal to 1 if the course is a single-credit elective course; 0 otherwise.
You seek evidence that since single-credit elective courses are relatively easy, they tend to get higher teaching evaluation scores than other courses. 新西兰经济代考
Here β1 is the difference in course evaluation scores between a one-credit course and multiple-credit courses. This means that β1 should be positive in our model (so, right- sided alternative).
H0 : β1 = 0 and H1 : β1 > 0
(ii)Model:
P B = β0 + β1P riceJ elly + u,
where P B is the demand for peanut butter, and P riceJ elly is the price of jelly.
You seek evidence that PB and jelly are complementary goods (the demand for one good is decreasing when the price of another good is increasing).
We seek evidence that as P riceJ elly increases, the demand for peanut butter, P B, goes down. This means that β1 should be negative in our model (so, left-sided alternative).
H0 : β1 = 0 and H1 : β1 < 0
(iii)Model:
BM I = β0 + β1exercise + u,
where BM I is individual’s Body Mass Index, and exercise is his/her amount of physical exercise per week (in hours).
You seek evidence that exercising is an important determinant of BMI.
Here we make no assumptions whether the relationship between exercising and BMI is positive or negative, but we expect here to be SOME relationship (which rules out β1 = 0 in our model), so we have a two-sided alternative.
H0 : β1 = 0 and H1 : β1 ƒ= 0
Question 3: 新西兰经济代考
(35 pts) The concept of purchasing power parity or PPP (“the idea that similar foreign and domestic goods should have the same price in terms of the same currency,” Abel,andB. Bernanke, Macroeconomics, 4th edition) suggests that the ratio of the Big Mac priced in the local currency to its U.S. dollar price should equal the exchange rate between the two countries.
After entering the data for 120 countries (where McDonald’s restaurants operate) into your spreadsheet program, you calculate the Big Mac exchange rate per U.S. dollarby dividing the price of a Big Mac in local currency by the U.S. price of a Big Mac.
To test for PPP, you plan to regress the actual exchange rate (XRate) on the “Big Mac exchange rate” (BM XRate):
XRate = β0 + β1BM XRate + u
(a)If PPP indeed holds, what does it imply for coefficients β0and β1? That is, if the ratio of the Big Mac priced in the local currency to the U.S. dollar price is equal the actual exchange rate between the two countries, what should be the relationship between actual and Big Mac exchange rates and what does it mean for the values of β0 and β1? 新西兰经济代考
If PPP holds, then actual exchange rate should be equal to the Big Mac exchange rate:
XRate = BM XRate. This implies that β0 = 0 and β1 = 1.
Next, you estimate the above regression model using OLS:
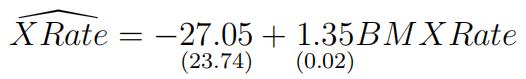
n = 120, R2 = 0.974
(b)Interpret the R2for this regression:
About 97% of total variation of the actual exchange rate is explained by (the variation of ) this predicted exchange rate.

(c)Interpret the slope coefficient for thisregression:
Across these 120 countries, an 1 unit (of local currency per U.S. dollar) increase in the Big Mac exchange rate is associated with a 1.35 units increase in the actual exchange rate.
(d)Test your null hypothesis about β0from part (a) at the 5% significance level. Justify the use of a one-sided or a two-sided test.
Our null hypothesis is H0 : β0 = 0. Economic theory does not tell us whether the intercept should be greater or less than zero if PPP does not hold, so we should use the two-sided alternative: Ha : β0 ƒ= 0. 新西兰经济代考
Since |t| = |−27.05| = 1.14 < 1.96, we fail to reject the null hypothesis that β0 = 0.
(e)Test your null hypothesis about β1from part (a) at the 5% significance level. Justify the use of a one-sided or a two-sided test.
Our null hypothesis is H0 : β1 = 1. Economic theory does not tell us whether the slope coefficient should be greater or less than one if PPP does not hold, so we should use the two-sided alternative: Ha : β1 ƒ= 1.
Since |t| = 1.35−1 = 17.5 > 1.96, we reject the null hypothesis that β1 = 1 against a two-sided alternative.
(f)Basedon your hypotheses tests, what is your conclusion: Does the PPP principle hold in real life?
It looks like the data does not support the PPP hypothesis.
(g)Findthe 99% confidence interval for the slope coefficient:
[1.35 ± 2.576 · 0.02] = [1.30, 1.40]Question 4:
(20 pts) A psychology professor wants to measure the effect of time pressureon exam scores, so he gives each of his 400 students the same exam, but some students get90 minutes to complete the exam, some get 105 minutes, and some get 120 minutes. Eachstudent is randomly assigned to one of the three examination times (say, by rolling a die). After the exams are graded, the professor plans to estimate the following model:
Scorei = β0 + β1T imei + ui
where Scorei is the number of points scored on the exam by student i, and T imei is the amount of time that student i had to complete the exam (so T imei = 90 or 105 or 120). 新西兰经济代考
(a)Explain what the uivariable represents here and give at least three specific examples of factors contained in the error term ui.
Error term ui represents all factors that can affect students’ exam score (other than time they’ve got to complete it). Some examples: time spend studying for the exam, learning ability, amount of sleep on the night before the exam, number of courses a student took that semester, attendance rate (percentage of classes attended), etc.
(b)Explain why in this model it may be reasonable to assume that E(ui|T imei) =
The time each student got to complete their exam was selected at random, so absolutely independent from any other factors that could have affected the score. Actually, here ui and T imei are independent, which in turn implies that E(ui|T imei) = 0.
(c)The estimated regressionis
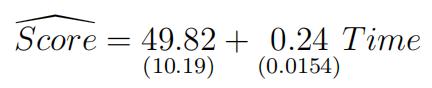
n = 400, R2 = 0.38
where standard errors are in parentheses.
(i)Whatis the predicted score for a student who is given 90 minutes to complete the exam? 100 minutes? 120 minutes?
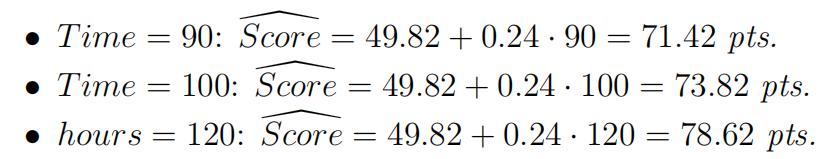
(ii)You seek evidence that time pressure has a negative effect on exam Specify the null and alternative hypotheses corresponding to that scenario and test your hypotheses at the 1% significance level. What is your conclusion?
If our theory is correct, then less time on the exam (lower T ime) will be associated with lower exam score, which means that β1 in our model is positive (T ime and Score move together). This is our alternative hypothesis, and the null hypothesis is that time pressure doesn’t affect exam outcomes (β1 is zero):
H0 : β1 = 0 vs Ha : β1 > 0
Here t = 0.240.0154= 15.58 > 2.33 0.24 0.0154 so we reject the null hypothesis in favor of our alternative and conclude that we do fifind evidence of negative effffect of time pressure.
Question 5: 新西兰经济代考
(10 pts) Management of a large fast-food chain wants to study the causal effect of competition on sales, so they propose estimating the following regression model:
Salesi = β0 + β1N umCompi + ui
where Salesi are sales (in $1000s) at store i, and N umCompi is the number of competi- tors within one mile of store i. They have data on 650 randomly selected stores.
(i)What are other factor (besides the number of competitors) that can affect fast- food sales? List at least three and explain why you think that these factors can influence fast-food
Some examples: 新西兰经济代考
population density in the area: if there are more people in the vicinity, the demand will be higher (so, higher sales) ;
proximity to public places (malls, business centers, colleges, etc) and events (concerts, games): more demand than in residential areas;
local marketing (think promotions and specials) and advertisement: helps to increase demand;
- weather: people may prefer to eat at home when the weather isbad;
- income level: people with higher income levels tend to eat less fast
(ii)Can any of those factor be correlated with the number of competitors?
Yes: e.g. higher population density and proximity to public places will attract more competitors; marketing can be used as a tool against local competition.

更多代写:澳洲Cs网课代考 gmat代写 英国网课代修代上 新西兰论文代写 英国媒体论文代写 留学生Research Proposal代写
