ECON G25 (MACROECONOMICS)
Macrodynamics and Growth
宏观动力学与增长代写 1.Consider the Solow growth model with technological progress at the rate g, population growth at the rate n and ···
Short answer type
1.
Consider the Solow growth model with technological progress at the rate g, population growth at the rate n and capital depreciation rate at the rate δ. The savings rate is s and the production function is given by F(K, AL) = Kα(AL)1-α, 0 < α < 1. Then y = f(k) = kα where y = Y/AL, k = K/AL, f(k) = F(k, 1). The notation is standard with Y output, K capital, A knowledge or technology and L labour. AL is effffective labour.
Answer the following questions based on this information.
a) Show that the aggregate production F(K, AL) = Kα(AL)1-α has constant returns to scale.
b) What is the intensive form of the production function? [Plot the intensive form of the production function!]
c) What is the steady state value of capital and output per unit of effffective labour?
d) What is the marginal product of capital in the steady state? Is it positive or negative?
e) What is the growth rate of aggregate capital and aggregate output in the steady state?
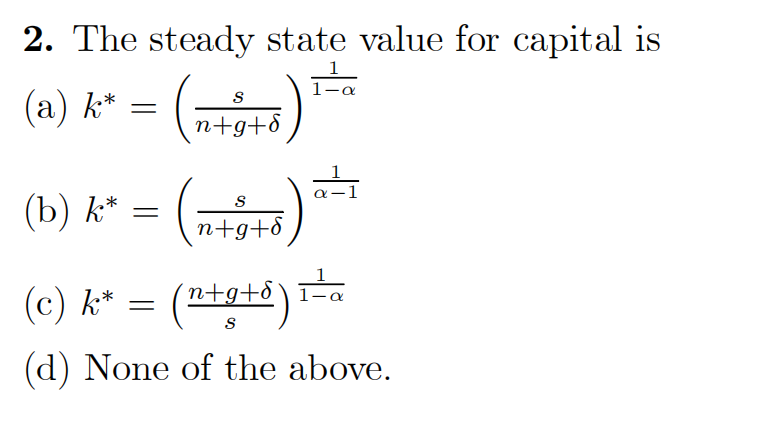
3.
Which of the following statements is correct?
a) An increase in the savings rate increases the steady state value of capital per unit of effffective labour in the Solow model.
b) An increase in the savings rate decreases the steady state value of capital per unit of effffective labour in the Solow model.
c) An increase in the population growth rate decreases output per unit of effective labour.
d) (a) and (c).
4. 宏观动力学与增长代写
Which of the following statements is correct?
a) The Ramsey model necessarily has an unique equilibrium.
b) The Solow model necessarily has an unique equilibrium.
c) The Diamond overlapping generations model necessarily has an unique equilibrium.
d) (a) and (b).
5.
Which of the following statements is correct?
a) Ricardian equivalence holds in the Ramsey model.
b) A fall in the discount rate of households increases output per unit of effective labour in the Diamond overlapping generations model with logarithmic utility and Cobb-Douglas production function.
c) The Diamond overlapping generations model may have multiple equilibria.
d) (a), (b) and (c).

8.
Which of the statements below may be true of c and k along the saddle path in the Ramsey model.
a) c and k are both decreasing.
b) c is decreasing and k is increasing.
c) c is increasing and k is decreasing.

10. 宏观动力学与增长代写
Which of the following reasons is not a cause for the failure of Ricardian equivalence.
a) Presence of credit constraints.
b) Presence of distortionary taxes.
c) Presence of infifinitely lived households.
d) None of the above.
11.
In the steady state of the Solow model, the rate of growth of output per unit of effective labour (y) is zero. True or False.
12. 宏观动力学与增长代写
Suppose, the rate of growth of population and the rate of depreciation is zero. The rate of growth of technology, on the other hand, g is positive. In the steady state of the Solow model, what is the rate of growth of aggregate output ( Y ). What is rate of growth of output per capita (Y/L)?
13. 宏观动力学与增长代写
Suppose there is a increase in the capital depreciation rate in the Solow model. What happens to capital and output per unit of effffective labour in the new steady state? Explain brieflfly the transition of the economy towards the new steady state?
14.
Consider the two period model of tax smoothing. It is optimal to allow tax revenues to rise during recessions according to this model. True or False?
15. 宏观动力学与增长代写
Suppose consumers live for two periods and receive endowments of Y1 and Y2 and pay lump-sum taxes T1 and T2 (where subscripts indicate periods 1 and 2). Consumers maximise a standard utility function U(C1 , C2) (where C1 and C2 are consumption levels). Consumers’ budget constraints in periods 1 and 2 are as follows
A1 = Y1 − T1 − C1 ,
C2 = Y2 − T2 + (1 + r)A1 ,
where A1 is the savings held at the end of period 1. Savings pay interest rate r.
The government spends G1 and G2. The government’s budget constraints in periods 1 and 2 are as follows
B1 = G1 − T1,
T2 = G2 + (1 + r)B1,
where B1 is the stock of government debt at the end of period 1. The government pays interest at rate r on its debt.
(a) Assume that taxes are cut in period 1 and they are raised in period 2 so as to continue to satisfy the government’s intertemporal budget constraint. Is the consumer’s optimal consumption choices affffected as a result of this change in tax policy. Explain brieflfly. [No proof is required; simply explain intuitively (in words)]
(b) Suppose consumers cannot borrow (so that consumption in period 1 must satisfy the additional constraint C1 ≤ Y1 − T1). How would this affffect your answer to part (a)?

更多代写:计算机lab作业代写 国际贸易Midterm代考 英国econ HOMEWORK代写 会计Accounting Essay代写 加拿大reference代写 弗里德哈德曼大学代写
