MATH2720 Multi-variable Calculus: Test Practice Pools
多变量微积分代写 Let z = (y2x2)2. Find all critical points of z. Identify whether they are local minimum, local maximum or saddle points.
Test 2 Practice Pool 多变量微积分代写
Disclaimer: There is no guarantee that your actual test questions will resemble these practice problems.
- Let
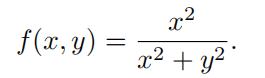
(a)Finda ray approaching the origin along which f (x, y) = 1.
(b)Finda ray approaching the origin along which f (x, y) = 0.
(c)Whatcan we say about the limit of lim(x,y)→(0,0) f (x, y)?
- Evaluate ifpossible:
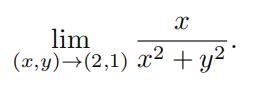
- Evaluate each of the following limits or show that it does notexist:
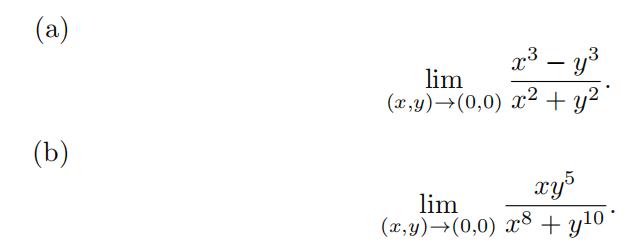
- Let
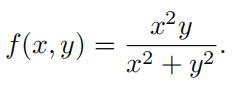
(a)Computefx using the defifinition.
(b)Computefy using the defifinition.
(c)Findd f (t, t)|t=0.
5.Findall first and second order partial derivatives of the following function and evaluate them at the given 多变量微积分代写
f (x, y, z) = ln(1 + exyz), (2, 0, −1).
- Findall first and second order partial derivatives of the following function and evaluate them at the given
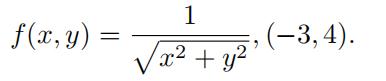
- Letf be any differentiable function of one Define z = f (x2 + y2). Does the equation
always hold?
yzx − xzy = 0
- Letw = f (x, y, t) with x and y depending on Suppose that at some point (x, y) and at some time t, the partial derivatives fx, fy, ft are equal 多变量微积分代写
to 2,3,and 5 respectively, while ![]() what is dw ? Is it the same with ft? why or why not?
what is dw ? Is it the same with ft? why or why not?
- Evaluatews and wt given w = x2 + y2 + z2, x = st, y = s cos t, z = s sint
- Suppose x2y +z = 1. Let w = sin x cos(2y). Find
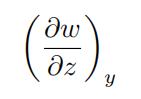
11.Letf 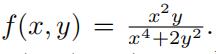 Find the equation of tangent plane to the surface z = f (x, y) at (−1, 1, 1 ). 多变量微积分代写
Find the equation of tangent plane to the surface z = f (x, y) at (−1, 1, 1 ). 多变量微积分代写
- Consider the surface z = f (x, y) defined implicitly by the equation xyz2+ y2z3 = 3 + x2. Use a 3–dimensional gradient vector to find the equation of the tangent plane to this surface at the point (1, 1, 2).
- Findall horizontal planes that are tangent to the surface with equation z = xye−(x +y )/2.
14.Find the directional derivative of f (x, y, z) = exyzin the direction of (0, 1, 1) at (0, 1, 1). 多变量微积分代写
- Let z = (y2x2)2. Find all critical points of z. Identify whether they are local minimum, local maximum or saddle points.
16.: Find all critical points for f (x, y) = x(x2+ xy + y2 9). Also find out which of these points give local maximum values for f(x, y), which give local minimum values, and which give saddle points.
17.Use the Second Derivative Test to find all values of the constant c for whichthe function z = x2 + cxy + y2 has a saddle point at (0, 0).
18.Findthe maximum and minimum values of f (x, y) = xy − x3y2when (x,y) runs over the square 0 ≤ x ≤ 1, 0 ≤ y ≤ 1.

更多代写:cs代写作业 midterm代考 Essay英文代写 Essay作业代写 学术法学论文代写 Math数学网课代考
