MATH 2170 Number Theory 1 Assignment 3
数论代写 As theory will be tested, quality of writing will be considering in marking. Only single display calculators are permitted.
SHOW ALL WORK to get full marks. Leave answers as exact answers. For example, leave it as fractions such as 1{7 as opposed to decimals such as 0.142857. Word problems should have sentence answers with units. Fractions should be in lowest terms. 数论代写
As theory will be tested, quality of writing will be considering in marking. Only single display calculators are permitted.
All assignments must be handed in via Crowdmark by 11:59pm on March 26th. Lateassignments will not be accepted. Failure to follow the instructions will result in a mark of 0.This assignment covers up to Section 3.2 in the textbook.
[6] 1.Let p be an odd prime. 数论代写
Show that if ![]() pmod pq for all primes q | p 1, then g is a primitive root. Use that result to determine whether 3 is a primitive root modulo 67.
pmod pq for all primes q | p 1, then g is a primitive root. Use that result to determine whether 3 is a primitive root modulo 67.

[6]4.(a) If c and d are quadratic non-residues modulo an odd prime p, then does x2cd pmod pq have a solution? You muust explain your reasoning. 数论代写
(b) If c is a quadratic non-residues modulo odd primes p and q, then does x2 c
pmod pqq have a solution? You muust explain your reasoning.
[6]5.Let p ? 5 be a prime. Find conditions on p such that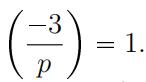 Use the result to show that there are infinitely many primes of the form 3n + 1. (cd)
Use the result to show that there are infinitely many primes of the form 3n + 1. (cd)
This assignment is out of 30 points.

更多代写:data structure代写 北美exam代考 Discussion辅导 北美argumentativ eessay代写 澳洲论文essay代写 算法与数据结构代写
