线性优化代写 Linear Optimization代写

ISyE/Math/CS/Stat 525 – Linear Optimization

Final exam

线性优化代写 No justifications needed. Mark “T” or “F”.Points per question: 0 points if wrong; 1/2 point if no answer; 1 point if correct.

READ THIS!

• This exam has a total of 4 problems and 40 points.
• Please write only one solution per question.
• The more clearly you write your answer, the better the chance that I can grade it accurately and give it full credit.
• Always justify your answers, unless otherwise stated.
• State properly any result that you use.
• Good Luck!

 

Question 1  线性优化代写

True or false …………………………………………………………. 10 points

No justifications needed. Mark “T” or “F”.

Points per question: 0 points if wrong; 1/2 point if no answer; 1 point if correct.

 

 

(b)_____

In the “column geometry” way of visualizing the simplex method, the reduced cost of variable x_j  is the vertical distance from the dual plane to the point (A_j , c_j ).

(c)_____

The dual of min {c′x | Ax ≤ b, x ≥ 0} is max {p′b | p′A ≤ c′ , p ≤ 0}.

(d)_____

Different bases may lead to the same basic solution for the primal problem, but to different basic solutions for the dual.

(e)_____

If f is a flow vector that satisfies the flow conservation constraints, C is a cycle, and θ is a scalar, then f + θh^C is also a flow vector that satisfies the flow conservation constraints.

(f)_____

The cost change resulting from the change of basis from f to f + θh^C is given by c′h^C .

(g)_____   线性优化代写

Consider an uncapacitated network flow problem, and assume that the optimal cost is finite. If all supplies b_i are integer, there exist an integer optimal flow vector, and an integer optimal solution to the dual problem.

(h)_____

Suppose that an algorithm takes polynomial time under the arithmetic model. Furthermore, suppose that on instances of size s, any integer produced in the course of the execution of the algorithm has size bounded by a polynomial in s. Then, the algorithm runs in polynomial time under the bit model as well.

(i)_____

The ellipsoid method solves the LP feasibility problem with integer data in polynomial time under the bit model.

(j)_____

Some LP problems with exponentially many constraint can be solved in polynomial time under the bit model.

 

Question 2  线性优化代写

The two-phase simplex method……………………………………….10 points

For two different linear programs (P₁) and (P₂) in standard form, during Phase I, we obtain the following tableaux (the original problem variables are x₁, . . . , x₄, and the artificial variables are y₁, y₂, y₃).

 

 

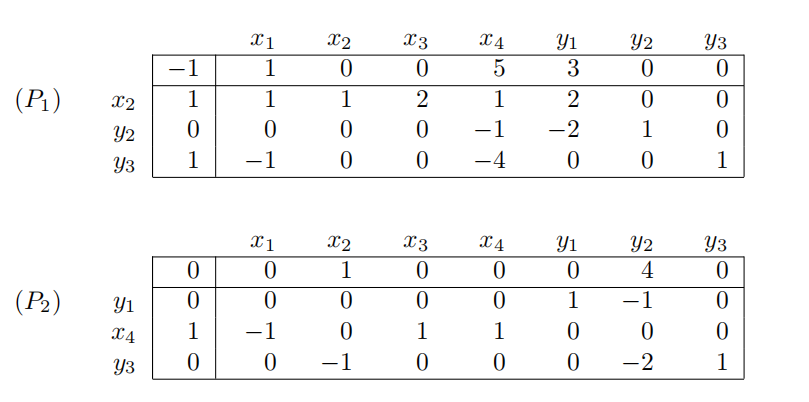
(a) (8 points) For each problem determine, if possible, a tableau to start Phase II, knowing that the objective function of both problems, to minimize, has coefffficients (2, 0, 0, 1).

__________________________________________________

__________________________________________________

__________________________________________________

 

(b) (2 points) Next, run the two-phase simplex method to termination by completing Phase II.

__________________________________________________

__________________________________________________

__________________________________________________

 

Question 3  线性优化代写

Duality proof ………………………………………………………… 10 points

Write a complete proof of Theorem 4.1: “If we transform the dual into an equivalent minimization problem and then form its dual, we obtain a problem equivalent to the original problem.” You can start with the following general linear programming problem as your primal:

min     c′x
s.t.       a_i′x ≥ b_i ,      i ∈ M₁
              a_i′x ≤ b_i ,      i ∈ M₂
              a_i′x = b_i ,      i ∈ M₃
              x_i  ≥ 0,      i ∈ I₁
              x_i  ≤ 0,      i ∈ I₂
             x_i  free,      i ∈ I₃

 

 

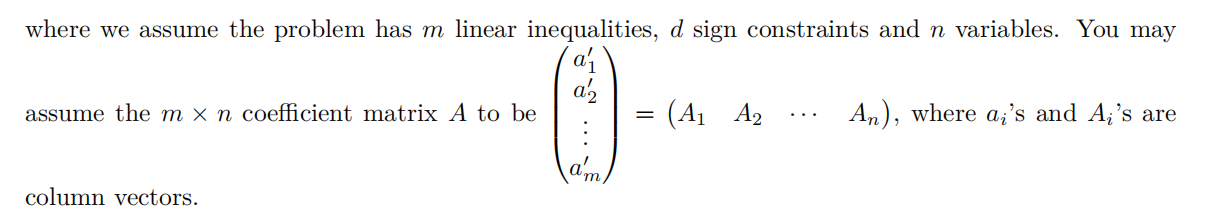
You should proceed by writing down the dual problem corresponding to the above one, then giving its equivalent minimization form of the dual, and writing down the dual of new minimization problem. You should briefly justify why these problems are equivalent as well.

__________________________________________________

__________________________________________________

__________________________________________________

 

Question 4  线性优化代写

Initial solution for network flow problems ……………………………. 10 points

In order to run the network simplex algorithm for an uncapacitated network flow problem, we need to obtain an initial basic feasible solution. In this exercise you will explain how such an initial basic feasible solution can be obtained. To answer this question, follow the three steps below briefly discussed in class, give all possible details, and justify every statement you make.

(a)(4 points) Construct an auxiliary directed graph by adding auxiliary arcs, and define the auxiliary problem over the new directed graph.

Hint: To define the auxiliary problem, in particular you need to define the costs of the arcs.

__________________________________________________

__________________________________________________

__________________________________________________

(b)(4 points) Explain how to obtain a basic feasible solution to the auxiliary problem without using the simplex method. (Don’t forget to prove that the solution you obtain is basic feasible!)

__________________________________________________

__________________________________________________

__________________________________________________

(c) (2 points) Explain how to obtain a basic feasible solution for the original problem from an optimal solution of the auxiliary problem.

__________________________________________________

__________________________________________________

__________________________________________________

 

 

其他代写： 英国代写 Exercise代写 finance代写 homework代写 北美作业代写 algorithm代写 analysis代写 app代写 assembly代写 C/C++代写 code代写 CS代写 cs作业代写 Data Analysis代写 essay代写

合作平台：essay代写 论文代写 写手招聘 英国留学生代写