BSc, MSci and MSc EXAMINATIONS (MATHEMATICS)
Probability and Statistics II
概率与统计II代写 (a) Write down the marginal density function fX(x).(b) State the law of iterated expectation, and use it to fifind the expectation of X.
1. 概率与统计II代写
Suppose X is a two-class mixture model, given as
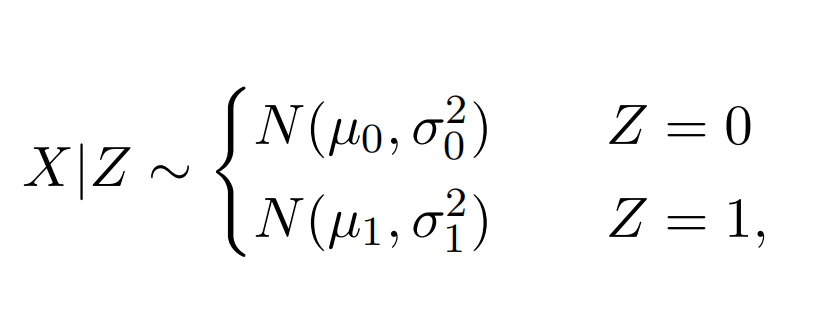
where Z ∼ Bernoulli(p).
(a) Write down the marginal density function fX(x).
(b) State the law of iterated expectation, and use it to fifind the expectation of X.
(c) State the law of total variance, and use it to fifind the variance of X.
2. 概率与统计II代写
The continuous random variable X has probability density function
fX(x|θ) = θxΘ–1 0 < x < 1, θ > 0.
A random sample (X1 , X2, . . . , Xn) is used to estimate the parameter θ.
(a) Defifine what it means for a random variable to be continuous.
(b) Determine the cumulative distribution of X.
(c) If θ is known, explain how a random sample from U ∼ Uniform (0, 1) could be used to produce a random sample with distribution X, proving any general results that you use.
(d) Compute the method of moments estimator of θ.
(e) Compute the maximum likelihood estimator of θ. (Remember to check explicitly that your estimator does indeed maximize the likelihood.)
(f) Let Y denote the method of moments estimator of θ. In the case n = 1, show that the sampling distribution of Y has density
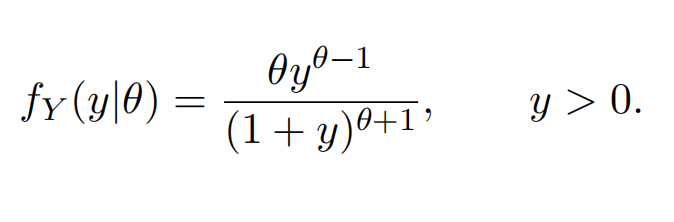
3. 概率与统计II代写
Consider two coins, of which one is a normal fair coin and the other is biased so that the probability of obtaining a Head is p > 1/2.
(a) Suppose p = 1 and a coin is selected at random and tossed n times, with tosses mutually independent. Evaluate the conditional probability that the selected coin is the normal one, given that the fifirst n tosses are all Heads. [Hint: You will need to use the Binomial distribution from M1S.]
(b) Now suppose 1/2 < p < 1 and that again, one of the coins is selected randomly and tossed n times. Let E be the event that the n tosses result in k Heads and n − k Tails, and let F be the event that the coin is fair. Find Pr(F|E).

其他代写: assignment代写 加拿大代写 python代写 report代写 paper代写 program代写 project代写 essay作业代写 作业代写 作业加急 英国代写 北美作业代写 homework代写 java代写 matlab代写 finance代写
