Signals and Systems
Final exam 2019 0603
信号与系统代写 1.Let be the function being 1 between and and 0everywhere else, that is, the function in the graph when ι = 1. Calculate its Fourier transform
1.Let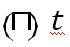
be the function being 1 between 
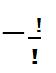and 
and 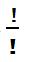0 信号与系统代写
everywhere else, that is, the function in the graph when ι = 1. Calculate its Fourier transform, and the convolution ⊓t (∗⊓)t () (the convolution with itself).
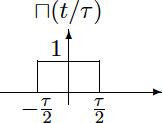
2.Given a discrete time linear system, the relation between the output y(n) and the input x(n) can always be put into a form like
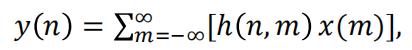
where ℎ(n, m) is a function of two variables. Please state what time invariance means for a linear system, and derive (prove) that the input-output relationship for a discrete time linear time-invariant system can be shown to have the form y(n) =
, where f(n) is a function in one variable only.
3.Given a discrete time signal x(n), we consider thefunction 信号与系统代写
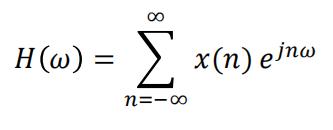
(assuming this is convergent for our signal x(n)). Please show that H(ω) is a periodic function in ω , and without any other assumption, please tell me what the period is. Then, explain that if we are given H(ω), how to recover x(n). (Notice that we defined H(ω) above by a linear mapping of x(n), so this means to find the inverse linear mapping of H(ω) that will give you x(n).)
4. For a continuous time linear time-invariant system, the input-output relation is the following (x(t) the input, y(t) the output): 信号与系统代写
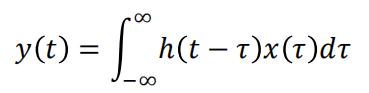
, where ℎ(t) is the impulse response function of the system. Please explain why a signal like eyωt is always an eigenvector of this linear map for any ω. Also, if Y(ω), X(ω) , and H(ω) are the Fourier transforms of y(t) , x(t) ,and h(t) , respectively. Please derive in detail the relation between Y(ω), X(ω) , and H(ω) , which means to reproduce the proof of the basic convolution property of Fourier transform. 信号与系统代写
- Let Sgn(t)be the function that equals 1 when t ≥ 0 , andequals −1 when t < 0. Compute its Fourier transform, and then use the differentiation rule to compute the Fourier transform of the delta function δ(t).
(each problem will be worth 20 points, and the total is 100 points)
其他代写：代写CS C++代写 java代写 matlab代写 web代写 homework代写 作业代写 物理代写 数学代写 考试助攻 paper代写 r代写 金融经济统计代写 lab代写
