STA256H5F
Probability and Statistics I
Assignment Nine
统计与概率代写 Please read Section 3.4 in the text. Also, look over your lecture notes. The following homework problems are not to be handed in.
Please read Section 3.4 in the text. Also, look over your lecture notes. The following homework problems are not to be handed in. They are preparation for Term Test 3 and the fifinal exam. Use the formula sheet.
1.
Let X have a moment-generating function MX (t) and let a be a constant. Show MaX (t) = MX (at).
2. 统计与概率代写
Let X have a moment-generating function MX (t) and let a be a constant. Show Ma+X (t) =eatMX (t).
3.
Let X1 and X2 be independent, discrete random variables, and let Y = g(X1) +h(X2). Show MY(t) = Mg(X1) (t) Mh(X2) (t). Because the random variables are discrete, you will add rather than integrating.
4. 统计与概率代写
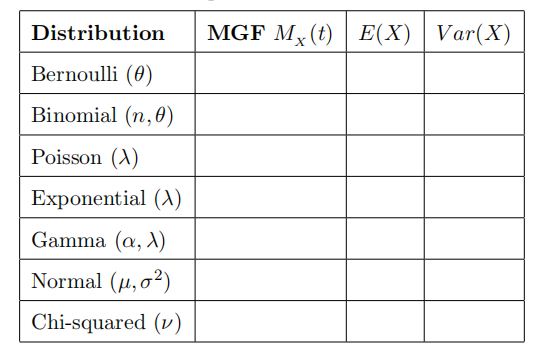
In the following table, derive the moment-generating functions (given on the formula sheet), and then use them to obtain the expected values and variances. To make the task shorter, notice that the Bernoulli is a special case of the binomial, and that the exponential and chisquared distributions are special cases of the gamma. Chi-squared is a gamma with α = v /2 and λ = ½ ; exponential is a gamma with α = 1. Do the general cases fifirst and then just write the answer for the special cases.
5.
Let X be a geometric random variable with parameter θ.
(a) Find the moment-generating function.
(b) Di↵erentiate to obtain E(X).


11. 统计与概率代写
Let Z ⇠ N(0, 1) and let Y = Z2. Find the distribution of Y using moment-generating functions.
12.
Let X be a degenerate random variable with P(X = µ) = 1.
(a) Find the moment-generating function.
(b) Di↵erentiate to obtain E(X) and V ar(X). Do these answers make sense?
(c) Comparing this to the moment-generating function of a normal, one can say that in a weird way, a degenerate distribution is normal with variance_____.
13.
Suppose that X and Y are discrete independent random variables with the following moment generating functions:
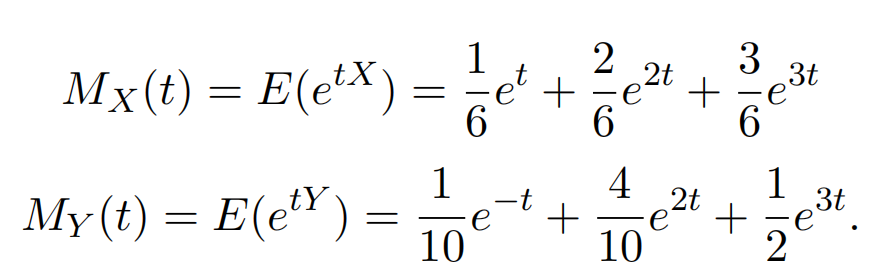
Using the moment generating function, fifind the distribution of
(a) Z = X + Y .
(b) U = X − Y .
14. 统计与概率代写
Let X and Y be discrete random variables such that
pX(x) =⅓ , x = −1, 0, 1
and
pY (y) =½ , y = 2, 4.
Let Z = X + Y .
(a) Using the probability mass functions of X and Y , fifind the probability mass function of Z.
(b) Find the moment generating function of Z.
(c) Using part (b), fifind the probability mass function of Z. Does your answer agree with (a)?
15. 统计与概率代写
Let X be a continuous random variable with pdf f(x) = ke–|x|, −∞<x<∞.
(a) Find the value of the constant k.
(b) Find the moment generating function of X.
(c) Find the mean and the variance of X.


其他代写:assignment代写 加拿大代写 作业代写 作业加急 英国代写 北美作业代写 homework代写 java代写 matlab代写 program代写 project代写 essay作业代写 finance代写 python代写 report代写 paper代写
