526 Discrete-state Stochastic Processes, Fall 2020.
Homework 1
Due: Saturday, September 26, 2020, by midnight eastern time.
The maximum number of points you can receive for this homework is 16.
526离散状态随机过程代写 526 Discrete-state Stochastic Processes, Fall 2020. Homework 1 Due: Saturday, September 26, 2020, by midnight eastern time.
1.(2 pts) 526离散状态随机过程代写
In unprofitable times corporations sometimes suspend dividend payments. Suppose that, after a dividend has been paid, the next quarter dividend will be paid withprobability 8. While after a dividend is suspended, the one for the next quarter will be suspended with probability 0.5. Also, we know that in the second quarter of 2015, 10% of the companies in the S&P500 index suspended their dividend payment. Assume that whether a company pays or retains the dividend can be modeled as a Markov chain. And that the assumptions of a “crowd of Markov chains” are satisfied.
a)What percentage of the companies in the S&P500 index will pay dividend in the second quarter of 2016?
b)What is the limiting fraction of companies paying dividends in quarter n, as n→ ∞?
2.(2 pts) 526离散状态随机过程代写
Census results reveal that in a country 1/3 of women work, and this fraction does not change from generation to generation. In addition, in any givengeneration, 40% of daughters of nonworking women will work. What percentage of daughters of working women will work (in any given generation)? You need to assume that each woman has exactly one daughter, that the Markov property holds for the corre- sponding process. (Which indicates whether a woman in nth generation is working). And that the assumptions of a “crowd of Markov chains” are satisfified.
3.(3 pts)
Do the following Markov chains converge to equilibrium? Provide precise arguments for your answer.

4.(3pts) 526离散状态随机过程代写
An individual has three umbrellas, some at his office, and some at If he is leaving home in the morning (or leaving work at night) and it is raining. He will take an umbrella, if there is one there. Otherwise, he gets wet. Assume that, independent of the past, it rains on each trip with probability 0.2. To formulate a Markov chain, let Xn be the number of umbrellas at his current location “before” he starts his n-th trip. Note that “current location” can either be home or office, depending on whether the trip is from home to office or vice versa.
a)Find the transition probabilities of this Markov chain.
b)Calculate the limiting fraction of time he gets wet.
5.(3 pts) 526离散状态随机过程代写
An auction-style exchange has two types of trading orders: standing (limit) andaggressive (market) The investors providing limit orders specify whether they want to sell or to buy. And the price at which they want to trade, and wait until one of the market orders executes their limit order. Of course, each market order can be of a “sell” or a “buy” type: a market sell order executes the standing buy orders. And a market buy order executes the standing sell orders. A popular predictor of the type of the next market order is the so-called “market imbalance”: a ratio of the total size of all standing buy orders to the total size of all standing sell orders. The higher is market imbalance, the more likely it is that the next market order is of a “buy” type.
Let time be measured in milliseconds, and let us focus on market buy orders only. 526离散状态随机过程代写
As- sume that the market imbalance can be in any of the three states: high (H), medium (M), or low (L). The imbalance may change in either direction for different reasons: because of an incoming market order. Or due the cancelation or addition of the stand-ing orders. If the imbalance is low, at the next time step it can either remain the same or increase to medium – both with probability 1/2 – and no market buy orders can arrive at this time step. If the imbalance is medium, at the next time step it can ei- ther decrease to low, with probability 1/3, or increase to high. When the imbalance increases from medium to high. It may happen for two different reasons: either due to the new market buy order that arrived within this time step.
Which happens with probability 1/2, or without any new market buy order arriving, which happens with probability 1/6. If the imbalance decreases from medium to low, no market buy or- ders can arrive within this time step. Finally, if the imbalance is high, at the next time step it either decreases to medium or stays at high – both with probability 1/2 – and, independent of this, a market order arrives with probability 2/3.
Consider Betty who always keeps a unit standing sell order in the exchange. Assume that every market buy order will execute Betty’s order (after which she will post another one). Every execution gives Betty 1 cent (e.g. from commission or from clever re-purchasing). What is Betty’s long-run profit per unit of time?
Hint: you need to construct the appropriate Markov chain, whose state space should include more than just H, M and L.
6(3pts)
Assume that the Markov chain with transition matrix p has a limiting distribu- tion π. Prove that for any initial distribution q, we have
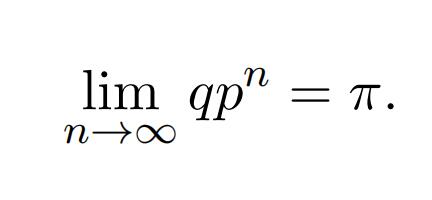

其他代写:homework代写 Exercise代写 algorithm代写 assignment代写 analysis代写 code代写 essay代写 app代写 assembly代写 CS代写 C++代写 C/C++代写 course代写 Data Analysis代写 data代写
