Math 272b: Numerical Differential Equations
数值微分方程代写 Exercise 1.1. Consider the Stokes equations in two dimensions. The bilinear form isB(u, v) = a(u, v) − b(v, p) − b(u, q) = (f, v)
Instructor: Randolph E. Bank Winter Quarter 2019
Homework Assignment #1
Due Friday, January 18, 2019
Exercise 1.1. Consider the Stokes equations in two dimensions. The bilinear form is
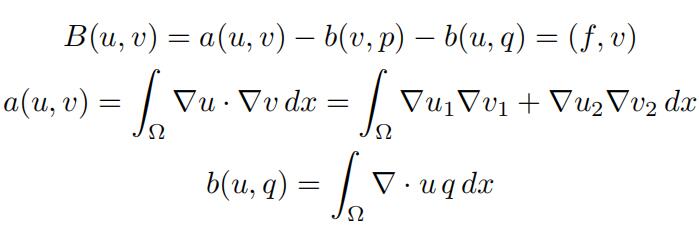
for u, v, ∈ H1 ×H1 and p, q ∈ L0. We discretize on a shape regular, quasi uniform, triangular mesh, using the mini-element: continuous piecewise linear finite elements with cubic bubble functions Pˆ1 × Pˆ1 ⊂ H1 × H1, and continuous piecewise linear finite elements with average0 0value zero P˜1 ⊂ L0.

1.On triangle t, let u be a linear polynomial and v be the cubic bubble function with support on t.Show: 数值微分方程代写
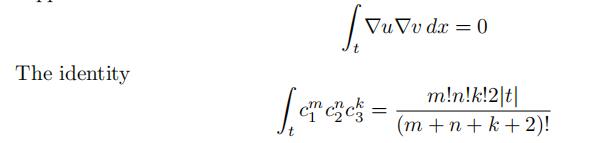
is helpful. Here the ci are baricentric coordinates (linear basis functions) on t and
v = 27c1c2c3. Remember c1 + c2 + c3 = 1 and ∇c1 + ∇c2 + ∇c3 = 0.
2.Show that the block 2 × 2 KKTsystem
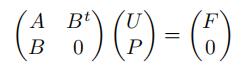
can be written as a block 5 × 5 system
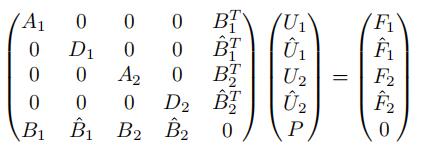
where the Ai are associated with the piecewise linear parts of the velocity, and the Di
are diagonal matrices associated with the cubic bubble functions.
3.Use static condensation (i.e., block Gaussian elimination) to reduce this system tothe 数值微分方程代写
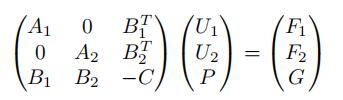
where C is symmetric and positive semi-definite. This reduced Schur complement system is the one usually solved in practice. The bubble function part of the solution is not computed; the bubble functions were introduced mainly for stability and not for accuracy.数值微分方程代写
- Show that the reduced system is actually a special case of the Petrov-Galerkin dis- cretization studied in class (i.e., the matrix C and the right hand side tt are equal to the corresponding terms in the Petrov-Galerkin formulation for a particular choice of constants). Thus the mini-element and the Petrov-Galerkin formulation stabilize the Stokes equations in a similar
数学272b:数值微分方程
授课教师:Randolph E.Bank Winter Quarter 2019
作业#1
到期日:2019年1月18日
练习1.1。考虑二维的斯托克斯方程。双线性形式为
B(u,v)= a(u,v)− b(v,p)− b(u,q)=(f,v)
a(u,v)=
Ω
··∇vdx =∫
∇u1∇v1+∇u2∇v2dx
b(u,q)=
Ω
u·u q dx
对于u,v,∈H1×H1和p,q∈L0。我们离散形状为规则的,准均匀的,三角形的
网格,使用微型元素:具有三次气泡的连续分段线性有限元
函数Pˆ1×Pˆ1⊂H1×H1,以及具有平均值的连续分段线性有限元
0 0
零值P〜1⊂L0。
1.在三角形t上,令u为线性多项式,v为在t上具有支持的三次气泡函数。表演:
身份
∫∇u∇vdx = 0
∫cmcnck = m!n!k!2 | t |
是有帮助的。此处ci是t和上的重心坐标(线性基函数)。
v = 27c1c2c3。记住c1 + c2 + c3 = 1且∇c1+∇c2+∇c3= 0。
2.显示块2×2 KKT系统
.ABtΣ.UΣ.FΣ
B 0 P = 0
可以写成5×5块系统
B1 Bˆ1 B2 Bˆ2 0 P 0
其中Ai与速度的分段线性部分相关,而Di
是与三次气泡函数关联的对角矩阵。
2数学272b
3,使用静态凝结(即阻止高斯消除)将该系统简化为B1 B2 -C P tt
其中C是对称且为正半定数。这种减少的Schur补体系统是通常在实践中解决的系统。该解决方案的气泡函数部分未计算;引入气泡函数主要是为了稳定性而不是准确性。
4.证明简化的系统实际上是在课堂上研究的彼得罗夫-加勒金离散化的特例(即,矩阵C和右手侧tt等于彼得罗夫-加勒金公式中特定项的对应项)选择常量)。因此,微型元素和Petrov-Galerkin公式以相似的方式稳定了Stokes方程。

其他代写:algorithm代写 analysis代写 app代写 assembly代写 assignment代写 C++代写 code代写 course代写 dataset代写 java代写 web代写 北美作业代写 编程代写 考试助攻 program代写 source code代写 dataset代写 金融经济统计代写 加拿大代写 jupyter notebook代写
