1、 简述
二叉查找树(Binary Search Tree,也叫二叉排序树,即Binary Sort Tree)可以适用多种多样动态性结合实际操作,它能够用于表明井然有序结合、创建数据库索引等,因此在具体运用中,二叉排序树是一种十分关键的算法设计。
从算法复杂度视角考虑到,我们知道,功效于二叉查找树上的操作过程(如搜索,插进等)的算法复杂度与树的高宽比正相关。对一个含n个连接点的完全二叉树,这种实际操作的最坏状况运作時间为O(log n)。但假如由于经常的删掉和插进实际操作,造成树衰退成一个n个连接点的线形链(这时即是一个单链表),则这种实际操作的最坏状况运作時间为O(n)。为了更好地摆脱之上缺陷,许多 二叉查找树的形变出現了,如红黑树、AVL树,Treap树等。
文中详细介绍了二叉查找树的一种改善算法设计–屈伸树(Splay Tree)。它的主要特点是不容易确保树一直是均衡的,但各种各样实际操作的分摊算法复杂度是O(log n),因此,从分摊复杂性上看,二叉查找树也是一种平衡二叉树。此外,对比于别的树形结构算法设计(如红黑树,AVL树等),屈伸树的室内空间规定与程序编写复杂性要小得多。
2、 操作过程
屈伸树的立足点是那样的:充分考虑可逆性基本原理(刚被浏览的內容下一次很有可能仍会被浏览,搜索频次多的內容很有可能下一次会被浏览),为了更好地使全部查找时间更小,被查頻率高的这些连接点理应常常处在挨近树杆的部位。那样,非常容易得想起下列这一计划方案:每一次搜索连接点以后对树开展重新构建,把被搜索的连接点搬移到树杆,这类自调节方式的二叉查找树便是屈伸树。每一次对屈伸树开展实际操作后,它均会根据转动的方式把被浏览连接点转动到树杆的部位。
为了更好地将当今被浏览连接点转动到树杆,大家一般 将连接点自底向上转动,直到该连接点变成树杆截止。“转动”的恰当之处便是不在弄乱数列中数据尺寸关联(指中序遍历結果是全序的)状况下,全部操作过程的分摊复杂性仍为O(log n)。
屈伸树关键有三种转动实际操作,各自为单转动,一字型转动和之字形转动。为了更好地便于表述,大家假定当今被浏览连接点为X,X的爸爸连接点为Y(假如X的爸爸连接点存有),X的爷爷连接点为Z(假如X的爷爷连接点存有)。
(1) 单转动
连接点X的父节点Y是根节点。这时候,假如X是Y的左小孩,大家开展一次左旋体实际操作;假如X 是Y 的右小孩,则大家开展一次左旋体实际操作。历经转动,X变成二叉查找树T的根节点,调节完毕。
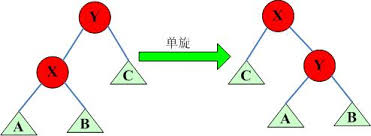
(2) 一字形转动
连接点X 的父节点Y并不是根节点,Y 的父节点为Z,且X与Y另外是分别父节点的左小孩或是另外是分别父节点的右小孩。这时候,大家开展一次左左转动实际操作或是右右转动实际操作。

(3) 之字形转动
连接点X的父节点Y并不是根节点,Y的父节点为Z,X与Y中一个是父亲连接点的左小孩而另一个是父亲连接点的右小孩。这时候,大家开展一次上下转动实际操作或是右左转动实际操作。

3、屈伸树区段实际操作
在具体运用中,屈伸树的中序遍历即是大家维护保养的数列,这就引出来一个难题,怎样在屈伸树中表明某一区段?例如我们要获取区段[a,b],那麼大家将a前边一个数相匹配的节点转到树杆,将b 后边一个节点相匹配的节点转到树杆的右侧,那麼根右侧的左子树就相匹配了区段[a,b]。缘故非常简单,将a 前边一个数相匹配的节点转到树杆后, a 及a 后边的数就在根的右子树枝,随后又将b后边一个节点相匹配的节点转到树杆的右侧,那麼[a,b]这一区段便是下面的图中B所显示的子树。

运用区段实际操作我们可以完成线段树的一些作用,例如回应对区段的了解(最高值,极小值等)。实际能够那样完成,在每一个节点纪录有关以这一节点为根的子树的信息内容,随后了解时先获取区段,再立即载入子树的基本信息。还能够对区段开展总体改动,这还要采用与线段树相近的延迟时间标记技术,即针对每一个节点,附加纪录一个或好几个标识,表明以这一节点为根的子树是不是被开展了某类实际操作,而且这类实际操作危害他的儿子节点的信息内容值,当开展转动和别的一些实际操作时相对地将标识往下传送。
与线段树对比,屈伸树作用更强劲,它能处理下列2个线段树不可以处理的难题:
(1) 在a插入一些数。方式是:最先运用要插进的数结构一棵屈伸树,然后,将a 转至根,并将a 后边一个数相匹配的节点转到根结点的右侧,最终将这棵新的子树挂到根右子节点的左子节点上。
(2) 删掉区段[a,b]内的数。最先获取[a,b]区段,立即删掉就可以。
4、完成
编码所有来源于【参考文献2】。
(1)转动实际操作
// node 为节点种类,在其中ch[0]表明左节点表针,ch[1]表明右节点表针
// pre 表明偏向爸爸的表针
// Rotate涵数用以(左/右)转动x->pre
void Rotate(node *x, int d) // 转动实际操作,d=0 表明左旋体,d=1 表明左旋体
{
node *y = x->pre;
Push_Down(y), Push_Down(x);
// 先将Y 节点的标识往下传送(由于Y 在上面),再把X 的标识往下传送
y->ch[! d] = x->ch[d];
if (x->ch[d] != Null) x->ch[d]->pre = y;
x->pre = y->pre;
if (y->pre != Null)
if (y->pre->ch[0] == y) y->pre->ch[0] = x;
else y->pre->ch[1] = x;
x->ch[r] = y, y->pre = x, Update(y); // 维护保养Y 节点
if (y == root) root = x; // root 表明整棵树的根节点
}
(2)splay实际操作
void Splay(node *x, node *f) // Splay 实际操作,表明把节点x 转到节点f 的下边
{
for (Push_Down(x) ; x->pre != f; ) // 一开始就将X 的标识下传
if (x->pre->pre == f) // 父节点的爸爸即是f,实行单转动
if (x->pre->ch[0] == x) Rotate(x, 1);
else Rotate(x, 0);
else
{
node *y = x->pre, *z = y->pre;
if (z->ch[0] == y)
if (y->ch[0] == x)
Rotate(y, 1), Rotate(x, 1); // 一字型转动
else
Rotate(x, 0), Rotate(x, 1); // 之字形转动
else
if (y->ch[1] == x)
Rotate(y, 0), Rotate(x, 0); // 一字型转动
else
Rotate(x, 1), Rotate(x, 0); // 之字形转动
}
Update(x); // 最终再维护保养X 节点
}
(3)将第k数量转到规定的部位
// 寻找处于中序遍历第k 个节点,并将其转动到节点f 的下边
void Select(int k, node *f)
{
int tmp;
node *t;
for (t = root; ; ) // 从根结点逐渐
{
Push_Down(t); // 因为要浏览t 的子节点,将标识下传
tmp = t->ch[0]->size; // 获得t 左子树的尺寸
if (k == tmp 1) break; // 得到t 即是搜索节点,撤出循环系统
if (k <= tmp) // 第k 个节点在t 左侧,向左走
t = t->ch[0];
else // 不然在右侧,并且在右子树中,这一节点不会再是第k 个
k -= tmp 1, t = t->ch[1];
}
Splay(t, f); // 实行转动
}
5、 运用
(1) 数列维护保养难题
题型:维护保养一个数列,适用下列几类实际操作:
1. 插进:在当今数列第posi 个数据插入tot 个数据;若在数列第一位插进,则posi 为0。
2. 删掉:从当今数列第posi 个数据逐渐持续删掉tot 个数据。
3. 改动:从当今数列第posi 个数据逐渐持续tot 个数据统一改动为c 。
4. 旋转:取下从当今数列第posi 个数据逐渐的tot 个数据,旋转后放进原先的部位。
5. 求饶:测算从当今数列第posi 个数据逐渐持续tot 个数据的和并輸出。
6. 求饶较大 子序列:求出当今数列中合较大 的一段子序列,并輸出较大 和。
(2) 轻量web服务器lighttpd中采用算法设计splay tree.
6、 参考文献
(1) 杨思雨《伸展树的基本操作与应用》
(2) Crash《运用伸展树解决数列维护问题》

