1. 简述
后缀数组是一种处理字符串数组难题的强有力专用工具。对比于后缀树,它更便于完成且占有运行内存更少。在具体运用中,后缀数组常常用以处理字符串数组相关的繁杂难题。
文中绝大多数內容节选自参考文献[1][2]。
2. 后缀数组
2.1 好多个定义
(1)后缀数组SA 是一个一维数组,它储存1..n 的某一排序SA[1],SA[2],……,SA[n],而且确保Suffix(SA[i]) < Suffix(SA[i 1]),1≤i<n。也就是将S 的n 个后缀名由小到大开展排列以后把安排好序的后缀名的开始部位依次放进SA 中。在其中,suffix(i)表明字符串数组s[i,i 1…n-1],即字符串数组s起起源于第i字符的后缀名。
(2)成绩二维数组Rank[i]储存的是Suffix(i)在全部后缀名中由小到大排序的“成绩”。
简易的说,后缀数组是“排几名的到底是谁?”,成绩二维数组是“你排几名?”。非常容易看得出,后缀数组和成绩二维数组为互逆运算。
(3)height 二维数组:界定height[i]=suffix(SA[i-1])和suffix(SA[i])的最多公共性作为前缀,也就是排行邻近的2个后缀名的最多公共性作为前缀。
(4) h[i]=height[rank[i]],也就是suffix(i)与在它前一名的后缀名的最多公共性作为前缀。
(5)LCP(i,j):对正整数i,j 界定LCP(i,j)=lcp(Suffix(SA[i]),Suffix(SA[j]),在其中i,j 均为1 至n 的整数金额。LCP(i,j)也就是后缀数组中第i 个和第j 个后缀名的最多公共性作为前缀的长短。在其中,涵数lcp(u,v)=max{i|u=v},也就是重新开始依次较为u 和v 的相匹配标识符,相匹配标识符不断相同的较大 部位,称之为这两个字符串数组的最多公共性作为前缀。
2.2 好多个特性
(1)LCP(i,j)=min{height[k]|i 1≤k≤j},换句话说,测算LCP(i,j)相当于了解一维数组height 中字符在i 1 到j 范畴内的全部原素的极小值。
证实略。
(2)针对i>1 且Rank[i]>1,一定有h[i]≥h[i-1]-1。
证实:设suffix(k)是排到suffix(i-1)前一名的后缀名,则他们的最多公共性作为前缀是h[i-1]。那麼suffix(k 1)将排到suffix(i)的前边(这儿规定h[i-1]>1,假如h[i-1]≤1,原式显而易见创立)而且suffix(k 1)和suffix(i)的最多公共性作为前缀是h[i-1]-1,因此suffix(i)与在它前一名的后缀名的最多公共性作为前缀最少是h[i-1]-1。依照h[1],h[2],……,h[n]的次序测算,并运用h 二维数组的特性,算法复杂度能够降至O(n)。
3. 后缀数组完成
这节得出高效率测算SA,Rank,height和h的优化算法
(1) 测算成绩二维数组Rank与后缀数组SA
选用倍增算法,先求出成绩Rank,随后在O(n)時间内求取后缀数组SA。用增长的方式对每一个标识符逐渐的长短为2^k 的子字符串数组开展排列,求出排行,即rank 值。k 从0 逐渐,每一次加1,当2m 超过n 之后,每一个标识符逐渐的长短为2^k 的子字符串数组便等同于全部的后缀名。而且这种子字符串数组都一定早已较为出尺寸,即rank 值中沒有同样的值,那麼这时的rank 值便是最终的結果。每一次排列都运用之前长短为2^(k-1) 的字符串数组的rank 值,那麼长短为2^k 的字符串数组就可以用2个长短为2^(k-1) 的字符串数组的排行做为关键词表明,随后开展基数排序,便得到了长短为2m 的字符串数组的rank 值。以字符串数组“aabaaaab”为例子,全部全过程如下图所显示。在其中x、y 是表明长短为2m 的字符串数组的2个关键词。
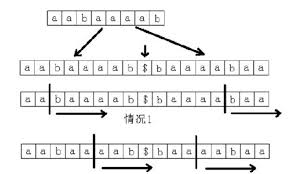
(2) 测算二维数组h
能够令i从1 循环系统到n依照以下方式先后计算h[i]:
若 Rank[i]=1,则h[i]=0。标识符较为频次为0。
若 i=1 或是h[i-1]≤1,则立即将Suffix(i)和Suffix(Rank[i]-1)从第一个标识符逐渐先后较为直至有标识符不同样,从而测算出h[i]。标识符较为频次为h[i] 1,不超过h[i]-h[i-1] 2。
不然,表明i>1,Rank[i]>1,h[i-1]>1,依据特性2,Suffix(i)和Suffix(Rank[i]-1)最少有前h[i-1]-1 字符是同样的,因此标识符较为能够从h[i-1]逐渐,直至某一标识符不同样,从而测算出h[i]。标识符较为频次为h[i]-h[i-1] 2。
可求取最终算法复杂度为O(n)。
4. 后缀数组运用
4.1 单独字符串数组有关难题
(1) 可重合最多反复子串。给出一个字符串数组,求最多反复子串,这两个子串能够重合。
『分析』只需规定height 二维数组里的最高值就可以。
(2) 不能重合最多反复子串。给出一个字符串数组,求最多反复子串,这两个子串不可以重合。
『分析』先二分回答,把题型变为判断性的问题:分辨是不是存有2个长短为k 的子串是同样的,且不重合。处理这个问题的重要還是运用height 二维数组。把排列后的后缀名分为若干组,在其中每一组的后缀名中间的height 值都不小于k。比如,字符串数组为“aabaaaab”,当k=2 时,后缀名分为了4 组:

非常容易看得出,有期待变成最多公共性作为前缀不小于k 的2个后缀名一定在同一组。随后针对每一组后缀名,只需要分辨每一个后缀名的sa 值的最高值和极小值之差是不是不小于k。如果有一组考虑,则表明存有,不然不会有。全部作法的算法复杂度为O(nlogn)。
(3) 可重合的k 次最多反复子串。给出一个字符串数组,求最少出現k 次的最多反复子串,这k 个子串能够重合。
『分析』 先二分回答,随后将后缀名分为若干组。不一样的是,这儿要分辨的是是否有一个组的后缀名数量不小于k。如果有,那麼存有k 个同样的子串符合条件,不然不会有。这一作法的算法复杂度为O(nlogn)。
(4) 最多回文子串。给出一个字符串数组,求最多回文子串。
『分析』 将全部字符串数组相反写在原字符串数组后边,正中间用一个独特的标识符分隔。那样就把难题变成了求这一新的字符串数组的某2个后缀名的最多公共性作为前缀。

(5) 持续反复子串。给出一个字符串数组L,已经知道这一字符串数组是由某一字符串数组S 反复R 次而获得的,求R 的最高值。
『分析』穷举法字符串数组S 的长短k,随后分辨是不是考虑。分辨的情况下,首先看字符串数组L 的长短可否被k 整除,再看suffix(1)和suffix(k 1)的最多公共性作为前缀是不是相当于n-k。在了解最多公共性作为前缀的情况下,suffix(1)是固定不动的,因此RMQ难题沒有必需做全部的预备处理, 只要求出height 二维数组中的每一个数到height[rank[1]]中间的极小值就可以。全部作法的算法复杂度为O(n)。
(6) 反复频次数最多的持续反复子串。给出一个字符串数组,求反复频次数最多的持续反复子串。
『分析』先穷举法长短L,随后求长短为L 的子串数最多能持续出現几回。最先持续出現1 次是毫无疑问能够的,因此这儿只考虑到最少2 次的状况。假定在原字符串数组中持续出現2 次,记这一子字符串数组为S,那麼S 毫无疑问包含了标识符r[0], r[L], r[L*2],r[L*3], ……中的某邻近的2个。因此只需要看标识符r[L*i]和r[L*(i 1)]向前和往后面各能配对到多远,记这一总长为K,那麼这儿连续出現了K/L 1 次。最终看最高值多少钱。、

穷举法长短L 的时间n,每一次测算的时间n/L。因此全部作法的算法复杂度是O(n/1 n/2 n/3 …… n/n)=O(nlogn)。
4.2 2个字符串数组有关难题
(1) 最多公共性子串。给出2个字符串数组A 和B,求最多公共性子串。
『分析』先将第二个字符串数组写在第一个字符串数组后边,正中间用一个沒有出現过的标识符分隔,再求这一新的字符串数组的后缀数组。当suffix(sa[i-1]) 和suffix(sa[i])并不是同一个字符串数组中的2个后缀名时,max{height[i]}才算是符合条件
(2) 长短不小于k 的公共性子串的数量。给出2个字符串数组A 和B,求长短不小于k 的公共性子串的数量(能够同样)。
『分析』理论依据是测算A 的全部后缀名和B 的全部后缀名中间的最多公共性作为前缀的长短,把最多公共性作为前缀长短不小于k 的一部分所有加起來。先将2个字符串数组连起來,正中间用一个沒有出現过的标识符分隔。按height 值排序后,下面的工作中就是迅速的统计分析每一组中后缀名中间的最多公共性作为前缀之和。扫描仪一遍,每碰到一个B 的后缀名就统计分析与前边的A 的后缀名能造成多少个长短不小于k 的公共性子串,这儿A 的后缀名必须用一个简单的栈来高效率的维护保养。随后对A 也那样做一次。
4.3 好几个字符串数组有关难题
(1) 不小于k 个字符串数组中的最多子串。给出n 个字符串数组,求出現在不小于k 个字符串数组中的最多子串。
『分析』将n 个字符串数组连起來,正中间用不同样的且沒有出現在字符串数组中的标识符分隔,求后缀数组。随后二分回答:将后缀名分为若干组,分辨每一组的后缀名是不是出現在不小于k 个的原串中。这一作法的算法复杂度为O(nlogn)。
(2) 每一个字符串数组最少出現2次且不重合的最多子串。给出n 个字符串数组,求在每一个字符串数组中最少出現2次且不重合的最多子串。
『分析』作法和上题如出一辙,也是先将n 个字符串数组连起來,正中间用不同样的且沒有出現在字符串数组中的标识符分隔,求后缀数组。随后二分回答,再将后缀名排序。分辨的情况下,需看是不是有一组后缀名在每一个原先的字符串数组中最少出現2次,而且在每一个原先的字符串数组中,后缀名的起止部位的最高值与极小值之差是不是不小于当今回答(分辨可否保证不重合,假如题型中沒有不重合的规定,那麼无需做此分辨)。这一作法的算法复杂度为O(nlogn)。
(3) 出現或翻转后出現在每一个字符串数组中的最多子串。给出n 个字符串数组,求出現或翻转后出現在每一个字符串数组中的最多子串。
『分析』这题不一样的地区取决于要分辨是不是在翻转后的字符串数组中出現。实际上这并沒有增加题型的难度系数。只必须先将每一个字符串数组都相反写一遍,正中间用一个互相同样的且沒有出現在字符串数组中的标识符分隔,再将n 个字符串数组所有连起來,正中间也是用一个互相同样的且沒有出現在字符串数组中的标识符分隔,求后缀数组。随后二分回答,再将后缀名排序。分辨的情况下,需看是不是有一组后缀名在每一个原先的字符串数组或翻转后的字符串数组中出現。这一作法的算法复杂度为O(nlogn)。
5. 小结
后缀数组事实上能够当作后缀树的全部叶节点依照从左往右的顺序排序放进二维数组中产生的,因此后缀数组的主要用途不太可能超过后缀树的范畴。乃至可以说,假如不配合LCP,后缀数组的运用范畴是很狭小的。可是LCP 涵数相互配合下的后缀数组就十分强劲,能够进行大部分后缀树能够进行的每日任务,由于LCP 涵数事实上得出了随意2个叶子结点的近期公共性先祖,这些方面的內容大伙儿能够自主科学研究。
6. 参考文献
(1) 许智磊,IOI2004 国家集训队毕业论文《后缀数组》
(2) 罗穗骞,IOI2004 国家集训队毕业论文《后缀数组—处理字符串的有力工具》

