1、 简述
Trie树,又被称为字典树,英语单词搜索树或是前缀树,是一种用以迅速查找的多叉树形结构,如英语字母的字典树是一个26叉树,数据的字典树是一个10叉树。
Trie一词来源于retrieve,音标发音为/tri:/ “tree”,也有些人读为/traɪ/ “try”。
Trie树能够运用字符串数组的公共性作为前缀来节省储存空间。如下图所显示,该trie树用10个连接点储存了6个字符串数组tea,ten,to,in,inn,int:
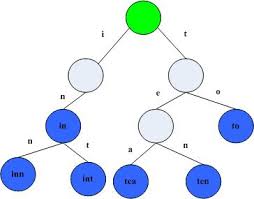
在该trie树中,字符串数组in,inn和int的公共性作为前缀是“in”,因而能够只储存一份“in”以节约室内空间。自然,假如系统软件中存有很多字符串数组且这种字符串数组基础沒有公共性作为前缀,则相对的trie树将十分耗费运行内存,这也是trie树的一个缺陷。
Trie树的基础特性能够梳理为:
(1)根节点不包含标识符,除根节点出现意外每一个连接点只包括一个字符。
(2)从根节点到某一个连接点,途径上历经的标识符相互连接,为该连接点相匹配的字符串数组。
(3)每一个连接点的全部子连接点包括的字符串数组不同样。
2、 Trie树的基础完成
英文字母树的插进(Insert)、删掉( Delete)和搜索(Find)都比较简单,用一个一重循环系统就可以,即第i 次循环系统寻找前i 个英文字母所相匹配的子树,随后开展相对的实际操作。完成这棵英文字母树,大家用最普遍的二维数组储存(静态数据开拓运行内存)就可以,自然还可以开动态性的表针种类(动态性开拓运行内存)。对于节点对孩子的偏向,一般有三种方式:
1、对每一个节点开一个英文字母集尺寸的二维数组,相匹配的字符是孩子所表明的英文字母,內容则是这一孩子相匹配在大二维数组上的部位,即型号;
2、对每一个节点挂一个链表,按一定次序纪录每一个孩子到底是谁;
3、应用左孩子右弟兄表示法纪录这棵树。
三种方式,各有特色。第一种易完成,但具体的室内空间规定很大;第二种,容易完成,室内空间规定相对性较小,但较为费时间;第三种,室内空间规定最少,但相对性费时间且不容易写。
下边得出动态性开拓运行内存的完成:
#define MAX_NUM 26
enum NODE_TYPE{ //"COMPLETED" means a string is generated so far.
COMPLETED,
UNCOMPLETED
};
struct Node {
enum NODE_TYPE type;
char ch;
struct Node* child[MAX_NUM]; //26-tree->a, b ,c, .....z
};
struct Node* ROOT; //tree root
struct Node* createNewNode(char ch){
// create a new node
struct Node *new_node = (struct Node*)malloc(sizeof(struct Node));
new_node->ch = ch;
new_node->type == UNCOMPLETED;
int i;
for(i = 0; i < MAX_NUM; i )
new_node->child[i] = NULL;
return new_node;
}
void initialization() {
//intiazation: creat an empty tree, with only a ROOT
ROOT = createNewNode(' ');
}
int charToindex(char ch) { //a "char" maps to an index<br>
return ch - 'a';
}
int find(const char chars[], int len) {
struct Node* ptr = ROOT;
int i = 0;
while(i < len) {
if(ptr->child[charToindex(chars[i])] == NULL) {
break;
}
ptr = ptr->child[charToindex(chars[i])];
i ;
}
return (i == len) && (ptr->type == COMPLETED);
}
void insert(const char chars[], int len) {
struct Node* ptr = ROOT;
int i;
for(i = 0; i < len; i ) {
if(ptr->child[charToindex(chars[i])] == NULL) {
ptr->child[charToindex(chars[i])] = createNewNode(chars[i]);
}
ptr = ptr->child[charToindex(chars[i])];
}
ptr->type = COMPLETED;
}
3、 Trie树的高級完成
能够选用双二维数组(Double-Array)完成。运用双二维数组能够大大的减少运行内存消耗量,实际完成关键点见参考文献(5)(6)。
4、 Trie树的运用
Trie是一种比较简单高效率的算法设计,但有很多的运用案例。
(1) 字符串数组查找
事前将已经知道的一些字符串数组(词典)的相关信息内容储存到trie树里,搜索此外一些不明字符串数组是不是出現过或是出現頻率。
举例说明:
@ 得出N 个英语单词构成的熟词汇表,及其一篇只用小写字母英文书写的文章内容,你要按最开始出現的次序写成全部没有熟词汇表中的单词。
@ 得出一个字典,在其中的英语单词为欠佳英语单词。英语单词均为小写字母。再得出一段文字,文字的每一行也由小写字母组成。分辨文字中是不是带有一切欠佳英语单词。比如,若rob是欠佳英语单词,那麼文字problem带有欠佳英语单词。
(2)字符串数组最多公共性作为前缀
Trie树运用好几个字符串数组的公共性作为前缀来节约储存空间,相反,在我们把很多字符串数组储存到一棵trie树处时,我们可以迅速获得一些字符串数组的公共性作为前缀。
举例说明:
@ 得出N 个小写字母英语字母串,及其Q 个了解,即了解某2个串的最多公共性作为前缀的长短多少钱?
解决方法:最先对全部的串创建其相匹配的英文字母树。这时发觉,针对2个串的最多公共性作为前缀的长短即他们所属节点的公共性先祖数量,因此,难题就转换为了更好地线下(Offline)的近期公共性先祖(Least Common Ancestor,通称LCA)难题。
而近期公共性先祖难题一样是一个經典难题,可以用下边几类方式:
1. 运用并查集(Disjoint Set),能够选用选用經典的Tarjan 优化算法;
2. 求出英文字母树的欧拉编码序列(Euler Sequence )后,就可以变为經典的极小值查看(Range Minimum Query,通称RMQ)难题了;
(有关并查集,Tarjan优化算法,RMQ难题,在网上有很多材料。)
(3)排列
Trie树是一棵多叉树,只需先序遍历整棵树,輸出相对的字符串数组就是按字典序排列的結果。
举例说明:
@ 让你N 个互相同样的仅由一个英语单词构成的英文名,使你将他们按字典序由小到大排列輸出。
(4) 做为别的算法设计和优化算法的輔助构造
如后缀树,AC自动机等
5、 Trie树复杂性剖析
(1) 插进、搜索的算法复杂度均为O(N),在其中N为字符串长度。
(2) 空间复杂度是26^n等级的,十分巨大(可选用双二维数组完成改进)。
6、 小结
Trie树是一种十分关键的算法设计,它在信息搜索,字符串匹配等行业有普遍的运用,另外,它也是许多 优化算法和繁杂算法设计的基本,如后缀树,AC自动机等,因而,把握Trie树这类算法设计,针对一名IT工作人员,看起来十分基本且必需!
7、 参考文献
(1)wiki:http://en.wikipedia.org/wiki/Trie
(2) 博闻《字典树的简介及实现》:
https://hi.baidu.com/luyade1987/blog/item/2667811631106657f2de320a.html
(3) 毕业论文《浅析字母树在信息学竞赛中的应用》
(4) 毕业论文《Trie图的构建、活用与改进》
(5) 博闻《An Implementation of Double-Array Trie》:
http://linux.thai.net/~thep/datrie/datrie.html
(6) 毕业论文《An Efficient Implementation of Trie Structures》

