代写 R code gamma distributed代写 numerical integration代写

Obligatory assignment 2 MSA101/MVE187, autumn 2018

代写 R code In the answers to the questions below, you should include your R code so that I can check that you have done correctly.The amount of electrical

Petter Mostad September 19, 2019

In the answers to the questions below, you should include your R code so that I can check that you have done correctly.代写 R code

1.The amount of electrical power P (v) produced by a wind turbine for a given wind speed v is described by the power curve of the turbine.代写 R code

For  a  2MW turbine we approximate the power curve with

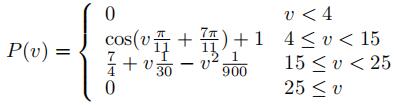
The wind speed at the location of the turbine will vary. Based on mete- orological records for this location, we model the wind speed as gamma distributed with parameters α = 0.8 and β = 1/6, where the gamma distibution has density

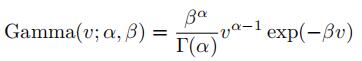
(a)Calculatethe probability that the turbine delivers power at any given time, Pr(P (v) > 0).代写 R code

(b)Computeby simulation the expected value, together with an approx- imate 95% confidence interval for the simulation accuracy, for the amount of power generated by the wind turbine. Show how your results depend on the sample size you choose.

(c)Compute the result of (b),  now using numerical integration,  either   by using discretization or the R functionintegrate.代写 R code

(d)Toimprove on the accuracy in (b) you would like to use importance sampling. Make a plot that is relevant for choosing a proposal density (instrumental density), and make such a choice.

(e)Nowrepeat (b) using importance sampling with your chosen proposal Compare the results with those of (b).代写 R code

(f)Use importance sampling to estimate the variance of the power pro- duction,Var(P (v)): Start by writing down the integral you woud like to compute

2.In a study of the number of death notices in the London Times on each dayin the interval 1910-1912 for women aged 80 and over,

it was noticed that the number of deaths did not follow a Poisson distribution as was expected.

The counts Y_i of days with i death notices is given in the table below:

(a)Assuming that the deaths each day follow a Poisson distribution, writedown the likelihood function for the Poisson density λ in terms of the observations Y_i  Compute the maximum likelihood esti- mate for λ. Plot the predicted counts using this λ together with the actual counts.

(b)As a small extension of the model above, we instead assume that, each day, there is a choice between two Poisson distributions, one withintensity λ₁ and the other with intensity λ₂. The probability for choosing λ₁ is p and the probability for choosing λ₂ is 1 − p. We now have a model with the three parameters, λ₁, λ₂, p. In order to work with this model, we add also variables Z₀, Z₁, . . . , Z₉, where Z_i is the (unobserved) count of days where λ₁ is used and where i deaths are observed. Thus 0 ≤ Z_i ≤ Y_i for i = 0, . . . , 9. Write down(a function proportional to) the likelihood for Y₀, . . . , Y₉, Z₀, . . . , Z₉ given the parameters λ₁, λ₂, p.代写 R code

(c)We  now assume we  have  a prior for the parameters p, λ₁, λ₂that    is a product of a uniform distribution on [0, 1] for p, a prior λ₁ ∼ Gamma(1, 1) for λ₁, and a prior λ₂   Gamma(1, 1) for λ₂.  Write 代写 R code codedown the posterior¹ for p given all the other observations and vari-ables.

(d)Find the posteriors for λ₁given all the other variables and pararme- ters, and similar for λ₂. 代写 R code

(e)Prove that the distribution of Z_igiven all parameters, all Y₀, . . . , Y₉, and all other Z_i variables, is Binomial. Find the parameters of this distribution.代写 R code

(f)Implmement a Gibbs sampler for the extended model above.   Use   the implementation to produce an approximate sample for the poste- rior distribution of the parameters p, λ₁, λ₂given the data y₀,. . . , y₉.

1The expressions ”write down the posterior” or ”find the posterior” mean that you should write down the formula for a function that is proportional to the posterior density, and, in the cases where the posterior is a distribution in a known parametric family, identify this family    and the correponding values of the parameters.

Visualize your results. Estimate the expected values of each of the parameters in this posterior.代写 R code

(g)(OPTIONAL) Use the expected values found above to simulatenew data, i.e., new deaths, for the same number of days as in the real data. Compare the predictions you get to the predictions obtained with the model in (a), and to the real data.代写 R code

其他代写：考试助攻 计算机代写 java代写 function代写 paper代写  web代写 编程代写 report代写 数学代写 algorithm代写 金融经济统计代写 finance代写 python代写 java代写 code代写 r代写 project代写 Exercise代写 matlab代写 作业帮助

合作平台：天才代写 幽灵代写 写手招聘 Essay代写