ECON 474-625: Numerical Methods for Economists
Numerical Methods代写 Assignment 3: Unconstrained Optimization Methods(Due date: Sunday February 25 before 11:30pm in Learn drop box)
Assignment 3: Unconstrained Optimization Methods
(Due date: Sunday February 25 before 11:30pm in Learn drop box)
This is an individual assignment. You can help each other, but the final result must be yours.
Question 1Numerical Methods代写
In this question, we want to compute the market demand using a two good market and a one dimen- tional unconstrained Newton method. You have to answer the question using expression and analitical derivatives. The market is composed of 1,000 consumers with the following utility function:
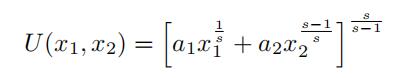
To generate you 1000 consumers, you will proceed as folows:

with the seed number replaced by your student id. Follow the following steps:
a)Write an expression for the utility function and a function that will return either the negative of the utility, the negative of the first derivative or the negative of the second derivarive (with respectto x1) at x1 when prices are p1 and p2, income is I and consumer spends all his The function would work as:

b)Write a function that returns the optimal x1and x2 using the Newton method. It should solve the following problem:Numerical Methods代写
l <- list(p1=5, p2=7, I=500, a1=1, a2=2, s=3)
getsol1(U=ces, x0=3,l=l)
## $sol
## x1 x2
## 1.734754 70.189461
##
## $niter
## [1] 7
Here x0 is the starting value for x1 because x2 is replaced by (I − p1x1)/p2, and the optimization is done with respect to x1.
c.The Newton method if not that reliable, expecially when there are restrictions on the possible values for x. For example, if we start too far from the solution, we get thefollowing
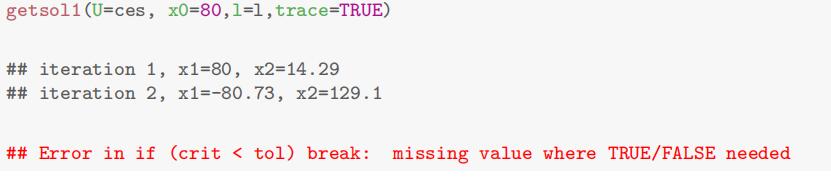
We can see that the Newton step is too large, which results in x1 being negative in the second step. That could be a problem because we want to solve 1,000 consumer problems with 1,000 different sets of parameters. Choosing a starting value that will make the algorithm converges for all consumers is impossible. In this step, you will modify your function so that it always converge for any sensible starting value (x0 must be less than I/p1). Here is what you will do. If x10 is the initial x1, the Newton method is:
x11 = x10 − s
where s = f j(x10)/f jj(x10). If x10 is less than the optimal x1, s will be negative and x10 willincrease. We don’t want it to increase too much and make x2 negative. If it happens, we want tolower the value of s. If x10 is greater than the optimal x1, s will be positive and x10 will decrease.Numerical Methods代写
If it decreases by too much, it will become negative. We can prevent that by decreasing s. Here is the modification you will add to your function: (i) As long as s > x0, then s = s/2. This will prevent x1 to become negative. (ii) As long as s < (x0 − I/p1), then s = s/2. This will prevent x2 to become negative. Something like the following (before computing the new x1) will do the job:
while (s>x0 | s<(x0-l$I/l$p1))
s <- s/2

The new function should now work for any x0:Numerical Methods代写
getsol2(U=ces, x0=80,l=l)
## $sol
## x1 x2
## 1.734754 70.189461
##
## $niter
## [1] 10
getsol2(U=ces, x0=99,l=l)
## $sol
## x1 x2
## 1.734754 70.189461
##
## $niter
## [1] 9
Once your function is stable, remove the argument x0 and set the starting value to a sensible value inside the function. Remember that x2 must be positive.
getsol(U=ces, l)Numerical Methods代写
## $sol
## x1 x2
## 1.734754 70.189461
##
## $niter
## [1] 8
c)Write a function that computes the total quantity demanded by your market (the sum of all 1,000 consumers) for a given set of prices p = p1, p2j. Try to make it work for any number of consumers. You would get something like:
library(parallel)Numerical Methods代写
marketD(p=c(3,6), par, U=ces, tol=1e-7, maxit=100, mc.cores=4)
## Market demand
## ***********************
## Number of consumers: 1000
## p1 = 3, p2 = 6
## x1 = 48968.99, x2 = 222166.76
## ***********************
Of course, you should all get different values as your par will be different. You are free to create a particular object with its print method if you want, but it is not required.
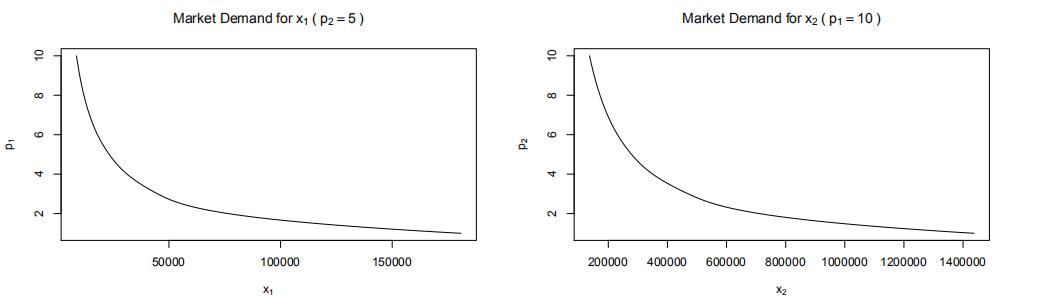
d)Write a function that plots the market demand of either x1for a given p2or x2 for a given p1. You would get something like:
plotMarket(which=1, otherPrice=5, from=1,Numerical Methods代写
to=10, n=10, U=ces, par=par)
plotMarket(which=2, otherPrice=10, from=1,
to=10, n=10, U=ces, par=par)
Market Demand for x1 ( p2 = 5 ) Market Demand for x2 ( p1 = 10 )
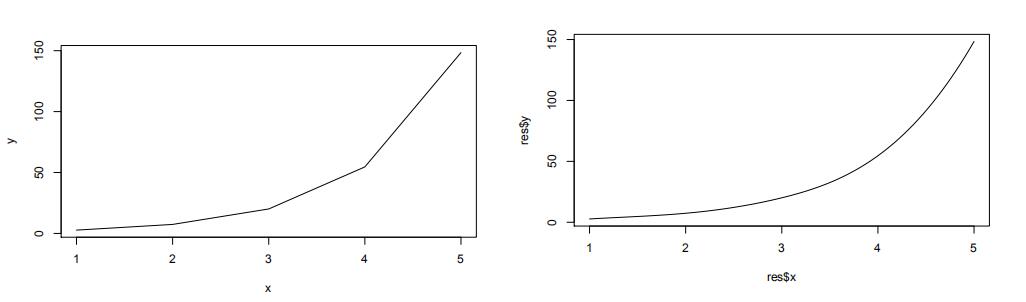
Hint: If you want to smooth a function with a few points, you can use spline(). For example:
x <- 1:5
y <- exp(x)
plot(x, y, type=”l”)
res <- spline(x, y, 500)
plot(res, type=”l”)
e)Comparethe effect of a 20% income on both demands when the other price is I am expecting something like
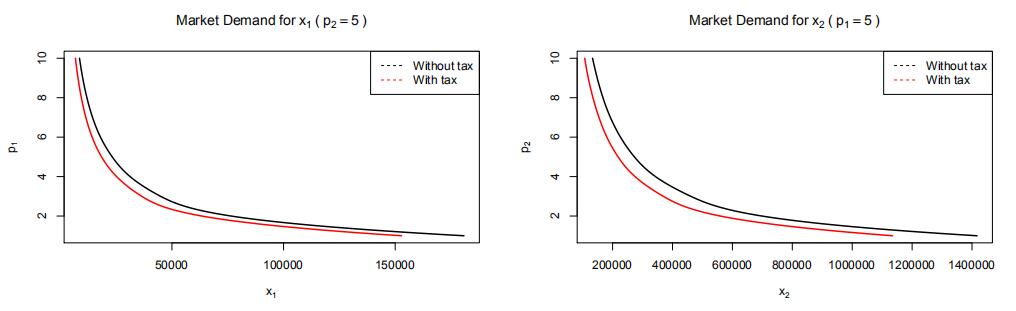
Question 2Numerical Methods代写
Estimate the ρ from the second assignment using the Newton method and numerical derivative. To do so, you need to have a function that depends on ρ, and returns the SSR. You can use part of your codes from the second assignment. Basically, for each ρ, you need to estimate the model:
(yt − ρyt−1) = (xt − ρxt−1)jβ + st
and return SSR = Pni=1 ˆ2t . You should get the following SSR:
set.seed(112233)
u <- arima.sim(n=200, model=list(ar=.7))
x1 <- rnorm(200)
x2 <- rnorm(200)
y <- 1+x1-x2+u
X <- cbind(Intercept=1,x1,x2)
(ssr <- SSR(rho=.5, y, X, “CO”))
## [1] 202.0671
(ssr <- SSR(rho=.5, y, X, “PW”))
## [1] 202.0674
After, you need a function that computes the first and second derivative of SSR(ρ).Numerical Methods代写
dssr <- dSSR(rho=.5, y, X, “CO”,h=.001))
## [1] -129.2444
(ddssr <- ddSSR(rho=.5, y, X, “PW”,h=.001))
## [1] 709.8033
Then, write the algorithm to minimize SSR. You should get:
getrho(rho0=.1, y, X, “CO”)
## $rho
## [1] 0.6819157
##
## $SSR
## [1] 190.3081Numerical Methods代写
##
## $niter
## [1] 3
getrho(rho0=.1, y, X, “PW”)Numerical Methods代写
## $rho
## [1] 0.6819152
##
## $SSR
## [1] 190.3086
##
## $niter

更多其他:C++代写 考试助攻 计算机代写 project代写 java代写 algorithm代写 代写CS 代码代写 function代写 作业代写 course代写 Data Analysis代写 app代写 物理代写
