CM20256 / CM50262 Functional Programmin
lambda-calculus代写 This coursework is about using the lambda-calculus as a programming language. Your so- lutions should be submitted
Coursework 2 – CM50262 version
Due: 6pm Wednesday May 2nd 2018
This coursework is about using the lambda-calculus as a programming language. Your so- lutions should be submitted via Moodle as a PDF file. You may write the solutions using appropriate software (LATEX, Word, etc.) or as a clearly legible handwritten document that you scan to PDF (the University printers have a scanning function). Throughout this assign- ment, you could of course write your solutions as pure lambda-terms, but that would be very hard to read. Make use of abbreviations to ensure that your solutions to these exercises are readable!lambda-calculus代写

Part 1 (Ordered triples 10%):lambda-calculus代写
It is useful in programming to collect multiple terms together as pairs, triples etc. Ordered triples may be encoded in the lambda-calculus as follows:
hM1, M2, M3i , Lp.p M1 M2 M3
The idea is that the variable p will be bound to a “projection” operator which will select one of M1 , M2 or M3 when the programmer wants to retrieve one of the elements of the triple.
a)Show that the following term Ø -reduces to M2:
hM1, M2, M3i (Lx.Ly.Lz.y)
You may assume that the terms M1 , M2 and M3 do not contain x , y or z as free variables.lambda-calculus代写
b)Defineterms ⇡1 , ⇡2 and ⇡3 such that for any terms M1 , M2 and M3 ,
⇡i hM1, M2, M3i !⇤Ø Mi
for i = 1, 2, 3 and demonstrate that ⇡2 works as intended.
Part 2 (Working with numbers – 40%):
We will now employ our ordered triples to define some useful functions that operate on the Church numerals.
a)Define a function T that operates on triples of Church numerals suchthat
Tha, b, ci !⇤Ø hb, c, c + 1i
and show that it works. You may make use of the successor function succ without explanation, as well as the ⇡i functions defined above.
b)Prove by induction on n that, for all Church numerals n,
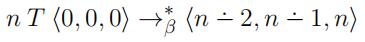
The.operation is subtraction curtailed at zero, that is:
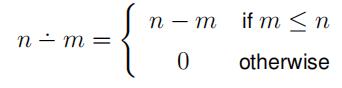
Part 3 (Fibonacci numbers – 10%):lambda-calculus代写
Below is the definition of a Haskell function that com- putes the Fibonacci numbers.
fib :: Int -> Int fib 0 = 1
fib 1 = 1
fib n = fib (n-1) + fib (n – 2)
Define a lambda-term F which implements this function, making use of the Y combinator to implement recursion and your function T to implement the calculations of n — 1 and n — 2 . You may make use of the following operations on Church numerals and Booleans
from the lectures: addition, test for zero, if-then-else.lambda-calculus代写
Part 4 (Research question – 40%):lambda-calculus代写
Write a short essay (around 2 pages) on combinatory logic and its relationship with the lambda-calculus and functional programming. You should:
- give a definition of what the combinators S , K and I are — this can be in terms of lambda-calculus if youlike
- argue that the combinators are as powerful as the full L-calculus
- provide some historical background on the discovery of combinatorylogic
- briefly discuss how combinators are relevant to the implementation of functional pro- gramminglanguages
- give references to support your claims and fifindings.lambda-calculus代写
This is a research question which deliberately goes beyond what we are covering in lec- tures. Please conduct your own research to find sources and material to help you answer it. Wikipedia is a good place to start, but you should avoid using it as a definitive reference. A really good answer would go beyond the material covered by the obvious Wikipedia pages.

更多其他:C++代写 java代写 r代写 Data Analysis代写 代码代写 金融代写 python代写 金融经济统计代写 web代写 物理代写 数学代写 考试助攻
