毫无疑问,函数预计是一个比参数预计要巨大得多的问题,虽然也是一个有趣的多的问题。这个问题在模子未知的尝试设计的建模中十分的常见,也是我正在进修的内容的一部门。
关于函数预计我想至少有这么几个问题是我们体贴的:1、我知道函数的一个或许的模子,需要预计函数的参数;2、我不知道它是一个什么模子,可是我想用一个不坏的模子刻画它;3、我不知道它是一个什么模子,我也不太体贴它的显式表达是什么,我只想知道它在没视察到的点的取值。这三个问题第一个是拟合可能叫参数预计,第二个叫函数迫近,第三个叫函数插值。从统计的角度来看,第一个是参数问题,剩下的长短参数的问题。
函数模子的参数预计
这类的问题有许多,一个较量典范的例子是柯布-道格拉斯函数( Y=L^alpha k^beta mu )。我们要预计参数常用的就是最小化残差平方和,假如是密度函数可能漫衍函数常用的步伐在加上矩预计与似然预计(MLE)两种步伐。
我们在这里先容一下R中的用于函数拟合的函数nls(),其挪用名目如下:
nls(formula, data, start, control, algorithm, trace, subset, weights, na.action, model, lower, upper, …)
其用法与线性回归函数lm()用法雷同,这里就不作过多先容了,我们来看几个例子来说明函数的用法:
景象一:指数模子
模仿模子( y=x^beta+varepsilon ),这里假设( beta=3 )
len <- 24
x <- runif(len, 0.1, 1)
y <- x^3 + rnorm(len, 0, 0.06)
ds <- data.frame(x = x, y = y)
str(ds)
## 'data.frame': 24 obs. of 2 variables:
## $ x: num 0.238 0.482 0.787 0.145 0.232 ...
## $ y: num 0.0154 0.12048 0.56788 0.10287 -0.00321 ...
plot(y ~ x, main = "Known cubic, with noise")
s <- seq(0, 1, length = 100)
lines(s, s^3, lty = 2, col = "green")
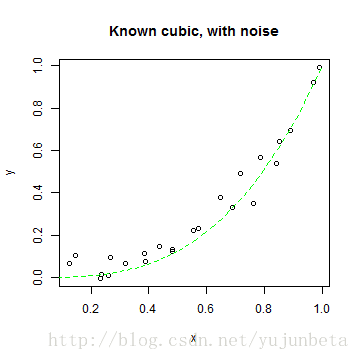
利用函数nls预计参数( beta )
m <- nls(y ~ I(x^power), data = ds, start = list(power = 1), trace = T)
## 1.637 : 1
## 0.2674 : 1.847
## 0.07229 : 2.464
## 0.06273 : 2.656
## 0.06264 : 2.677
## 0.06264 : 2.678
## 0.06264 : 2.678
summary(m)
##
## Formula: y ~ I(x^power)
##
## Parameters:
## Estimate Std. Error t value Pr(>|t|)
## power 2.678 0.117 22.9 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.0522 on 23 degrees of freedom
##
## Number of iterations to convergence: 6
## Achieved convergence tolerance: 6.07e-06
虽然,也可以双方取对数,通过最小二乘来处理惩罚这个问题。其R代码如下:
model <- lm(I(log(y)) ~ I(log(x)))
summary(model)
##
## Call:
## lm(formula = I(log(y)) ~ I(log(x)))
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.8016 -0.2407 -0.0368 0.2876 1.4164
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -0.446 0.233 -1.91 0.07 .
## I(log(x)) 1.680 0.251 6.69 1.3e-06 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.695 on 21 degrees of freedom
## (1 observation deleted due to missingness)
## Multiple R-squared: 0.681, Adjusted R-squared: 0.666
## F-statistic: 44.8 on 1 and 21 DF, p-value: 1.27e-06
假如这个模子尚有常数项,双方取对数就欠好使了,不外,我们的nls函数照旧能办理的。
景象二:含常数项的指数模子
模仿模子( y=x^beta+mu +varepsilon ),这里假设( beta=3,mu=5.2 )
len <- 24
x <- runif(len)
y <- x^3 + 5.2 + rnorm(len, 0, 0.06)
ds <- data.frame(x = x, y = y)
str(ds)
## 'data.frame': 24 obs. of 2 variables:
## $ x: num 0.277 0.831 0.127 0.464 0.734 ...
## $ y: num 5.17 5.79 5.22 5.37 5.64 ...
plot(y ~ x, main = "Known cubic, with noise")
s <- seq(0, 1, length = 100)
lines(s, s^3, lty = 2, col = "green")
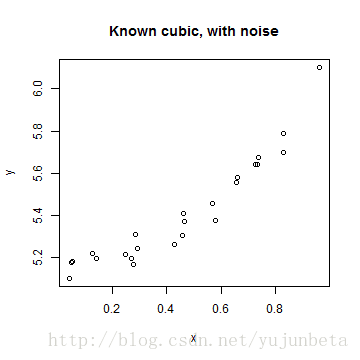
利用nls函数预计如下:
rhs <- function(x, b0, b1) {
b0 + x^b1
}
m.2 <- nls(y ~ rhs(x, intercept, power), data = ds, start = list(intercept = 0,
power = 2), trace = T)
## 632.5 : 0 2
## 0.05006 : 5.171 2.331
## 0.04934 : 5.173 2.395
## 0.04934 : 5.174 2.404
## 0.04934 : 5.174 2.404
## 0.04934 : 5.174 2.405
## 0.04934 : 5.174 2.405
summary(m.2)
##
## Formula: y ~ rhs(x, intercept, power)
##
## Parameters:
## Estimate Std. Error t value Pr(>|t|)
## intercept 5.1740 0.0184 281.5 < 2e-16 ***
## power 2.4046 0.1775 13.6 3.7e-12 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.0474 on 22 degrees of freedom
##
## Number of iterations to convergence: 6
## Achieved convergence tolerance: 1.67e-06
假如这时我们照旧回收最小二乘预计的步伐处理惩罚,那么获得的功效是:
model <- lm(I(log(y)) ~ I(log(x)))
summary(model)
##
## Call:
## lm(formula = I(log(y)) ~ I(log(x)))
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.03703 -0.02483 -0.00204 0.01840 0.08087
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.72898 0.00915 188.89 < 2e-16 ***
## I(log(x)) 0.03816 0.00648 5.89 6.3e-06 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.0287 on 22 degrees of freedom
## Multiple R-squared: 0.612, Adjusted R-squared: 0.594
## F-statistic: 34.7 on 1 and 22 DF, p-value: 6.32e-06
我们可以将预计数据、真实模子、nls预计模子、最小二乘模子获得的功效展示在下图中,来拟合优劣有个直观的判定:
plot(ds$y ~ ds$x, main = "Fitted power model, with intercept", sub = "Blue: fit; magenta: fit LSE ; green: known")
lines(s, s^3 + 5.2, lty = 2, col = "green")
lines(s, predict(m.2, list(x = s)), lty = 1, col = "blue")
lines(s, exp(predict(model, list(x = s))), lty = 2, col = "magenta")
segments(x, y, x, fitted(m.2), lty = 2, col = "red")
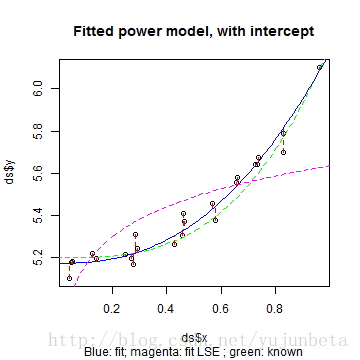
从图就可以看出,化为最小二乘的步伐不老是可行的。
景象三:分段函数模子
我们来看下面的模子:
f.lrp <- function(x, a, b, t.x) {
ifelse(x > t.x, a + b * t.x, a + b * x)
}
f.lvls <- seq(0, 120, by = 10)
a.0 <- 2
b.0 <- 0.05
t.x.0 <- 70
test <- data.frame(x = f.lvls, y = f.lrp(f.lvls, a.0, b.0, t.x.0))
test <- rbind(test, test, test)
test$y <- test$y + rnorm(length(test$y), 0, 0.2)
plot(test$y ~ test$x, main = "Linear response and plateau yield response", xlab = "Fertilizer added",
ylab = "Crop yield")
(max.yield <- a.0 + b.0 * t.x.0)
## [1] 5.5
lines(x = c(0, t.x.0, 120), y = c(a.0, max.yield, max.yield), lty = 2)
abline(v = t.x.0, lty = 3)
abline(h = max.yield, lty = 3)
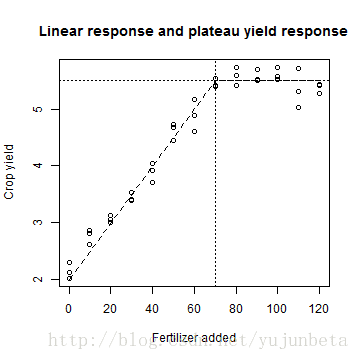
显然用一个线性模子办理不了,二次模子办理欠好,分段函数倒是一个很好的选择,那么在那边分别较量公道呢?我们照旧用nls函数来办理这个问题:
m.lrp <- nls(y ~ f.lrp(x, a, b, t.x), data = test, start = list(a = 0, b = 0.1,
t.x = 50), trace = T, control = list(warnOnly = T, minFactor = 1/2048))
## 32.74 : 0.0 0.1 50.0
## 7.352 : 2.16251 0.04619 59.34899
## 1.25 : 2.16251 0.04619 70.24081
## 1.116 : 2.15689 0.04639 72.09071
## 1.116 : 2.15689 0.04639 72.08250
summary(m.lrp)
##
## Formula: y ~ f.lrp(x, a, b, t.x)
##
## Parameters:
## Estimate Std. Error t value Pr(>|t|)
## a 2.15689 0.06562 32.9 <2e-16 ***
## b 0.04639 0.00157 29.6 <2e-16 ***
## t.x 72.08250 1.76996 40.7 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.176 on 36 degrees of freedom
##
## Number of iterations to convergence: 4
## Achieved convergence tolerance: 3.63e-09
绘图来看看拟合的靠得住性:
plot(test$y ~ test$x, main = "Linear response and plateau yield response", xlab = "Fertilizer added",
ylab = "Crop yield")
(max.yield <- a.0 + b.0 * t.x.0)
## [1] 5.5
lines(x = c(0, t.x.0, 120), y = c(a.0, max.yield, max.yield), lty = 2, col = "blue")
abline(v = t.x.0, lty = 3, col = "blue")
abline(h = max.yield, lty = 3, col = "blue")
(max.yield <- coefficients(m.lrp)["a"] + coefficients(m.lrp)["b"] * coefficients(m.lrp)["t.x"])
## a
## 5.501
lines(x = c(0, coefficients(m.lrp)["t.x"], 120), y = c(coefficients(m.lrp)["a"],
max.yield, max.yield), lty = 1)
abline(v = coefficients(m.lrp)["t.x"], lty = 4)
abline(h = max.yield, lty = 4)
text(120, 4, "known true model", col = "blue", pos = 2)
text(120, 3.5, "fitted model", col = "black", pos = 2)
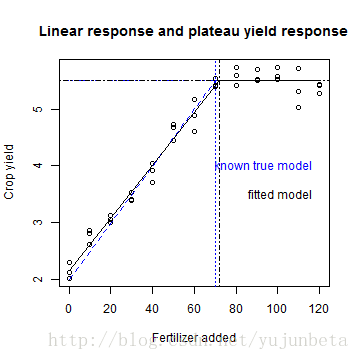
可以看到拟合的功效照旧不错的。这也显示了nls函数的优秀之处,险些可以拟合所有的持续函数,哪怕他们存在不行微的点。它的算法是怎么样的我没有深究,不外光是分段线性模子,CART算法但是一个不错的选择,模子树(model tree)就是拟合这种模子的极好的选择。
最近在整理呆板进修的条记,model tree的R代码确实是写好了,不外由于人懒,敲字慢,最终也没形成文字发出来与各人分享。
我们对参数预计或许就先容这么多,关于矩预计,极大似然预计可以拜见之前的博文《R语言与点预计进修条记(矩预计与MLE)》.虽然,假如一个函数疏散掉已知部门是一个密度函数的话,矩预计与极大似然仍然是可用的,如你想预计函数( f(x)=e^{-(x-mu)^2} )中的参数( mu )。
