生命游戏是英国数学家John Horton Conway在1970年发现的细胞自念头(cellular automaton)。它最初于1970年10月在《科学美国人》杂志中呈现。生命游戏是在一个二维矩形世界中,这个世界中的每个方格居住着一个细胞。细胞的生命状态只有在世或灭亡两种。细胞在下一个时刻的存亡取决于相邻八个方格中在世细胞的数量。假如相邻方格在世的细胞数量过多,这个细胞会因为资源匮乏而在下一个时刻死去;相反,假如周围活细胞过少,这个细胞会因太孑立而死去。
个中一种较为富厚的设定有如下四条:
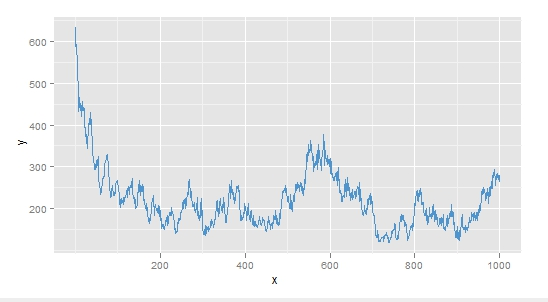
按照这些资料,笔者在R中运行了相应的代码,首先运行1000次的演变进程,记录每个时间点上细胞的总数,按照这些变革的数字可以获得如下的图形。可以看到一开始细胞过多而呈现大量灭亡,在靠近灭尽的时候又由于资源的空闲而大量繁殖,但繁殖存在一个上限,之后存活数目呈上下振荡趋势。
生命游戏是英国数学家John Horton Conway在1970年发现的细胞自念头(cellular automaton)。它最初于1970年10月在《科学美国人》杂志中呈现。生命游戏是在一个二维矩形世界中,这个世界中的每个方格居住着一个细胞。细胞的生命状态只有在世或灭亡两种。细胞在下一个时刻的存亡取决于相邻八个方格中在世细胞的数量。假如相邻方格在世的细胞数量过多,这个细胞会因为资源匮乏而在下一个时刻死去;相反,假如周围活细胞过少,这个细胞会因太孑立而死去。
个中一种较为富厚的设定有如下四条:
按照这些资料,笔者在R中运行了相应的代码,首先运行1000次的演变进程,记录每个时间点上细胞的总数,按照这些变革的数字可以获得如下的图形。可以看到一开始细胞过多而呈现大量灭亡,在靠近灭尽的时候又由于资源的空闲而大量繁殖,但繁殖存在一个上限,之后存活数目呈上下振荡趋势。
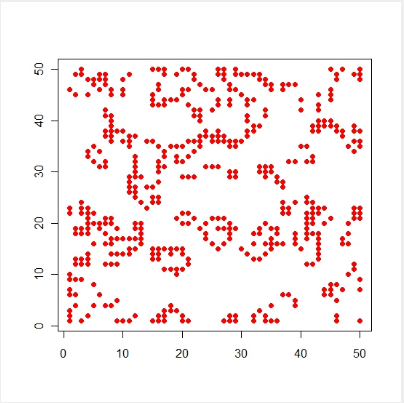
注:本文参考了wiki,以及《Introduction to Scientific Programming and Simulation Using R》第五章的习题。
R代码:
rm(list=ls())
#成立一个计较相近存活细胞数目标函数,并使边沿的细胞仍有八个邻人
neighbours <- function(A,i,j,n) {
left <- ifelse(j == 1,n,j-1)
right <- ifelse(j == n, 1, j+1)
up <- ifelse(i == 1, n, i-1)
down <- ifelse(i == n, 1, i+1)
nbrs <- sum(A[up,left] == 1,A[up,right] == 1,A[up,j] == 1,A[i,left] == 1, A[i,right] == 1,A[down,left] == 1,A[down,right] == 1,A[down,j] == 1)
return(nbrs)
}
n <- 50 #方阵的行数
A <- matrix(round(runif(n^2)),n,n) #初始化二维世界方阵
finished <- FALSE
while (!finished) { #反复举办演化,你需要用ESC退出
plot(c(1,n),c(1,n),type=’n’,xlab=”,ylab=”) #画图
for(i in 1:n) {
for (j in 1:n) {
if (A[i,j]==1) {
points(i,j,pch=16,col=’red’)
}
}
}
B <- A #将上期的信息存入本期矩阵B,并凭据条件修改B
for (i in 1:n) {
for (j in 1:n) {
nbrs <- neighbours(A,i,j,n)
if (A[i,j]==1) {
if ((nbrs ==2) | (nbrs==3)){
B[i,j] <- 1
} else {
B[i,j] <- 0
}
} else {
if (nbrs ==3) {
B[i,j] <- 1
} else {
B[i,j] <- 0
}
}
}
}
A <- B #将变革后的B矩阵存回到A中
}
