2012年4月11日①,在苏门答腊北部四周海疆产生了里氏8.6级地动,而就在一天之后,4月12日,在太平洋彼岸的墨西哥,又产生了里氏7.0级的地动。遐想2012世界末日的预言,不少人纷纷担忧起来,我们的地球是否已经走到了歼灭的边沿?同时,一些有关方面的专家也暗示,地球或者已经进入了地动频发期②。那么,我们是否可以借助一些根基的线性回归阐明要领,操作R软件,对近期地动产生的隔断做出阐明?又或实验对下一次大地动的时间做出简朴预测?本尝试的主要目标即是借助所进修过的根基常识,对上述两个问题做出解答。由于本领有限,如有不敷,但愿可以获得各人的指正以及辅佐。
一. 筹备事情:
1. 收集数据:
收集2011年1月1日至今(2011年4月12日)产生的所有地动数据③。为缩小研究范畴,只思量震级大于6级的地动。为消除余震对回归阐明的影响,解除所有余震。为提高回归阐明的精确性,只思量产生在环太平洋地动带的地动。获得如表1所示的141条地动数据。
个中,No, Year, Month, Day, Hour, Min, Second, Latitude, Longtitude, Depth, Magnitude, Location 各项别离暗示地动的编号(时间正序)、产生的年、月、日、时、分、秒、震级、震源的经度、维度、震源深度、震源所在。而Time 项暗示,以2011年1年1月1日0点整为时间起点,某次地动的产生时间,以秒为单元,记为Tn , (n=1,2,3,…,141)。而Time Diff 项,即为Tn-Tn-1 项的值 (n=2,3,…,141)。
2. 简化数据:
只保存表1中Time Diff 一项,成立表2。
3. 数据录入:
在R中成立timediff 变量以录入数据,代码如下:
Timediff=c(123801,210357,357455,300544,67428,356655,764495,1051871,240344,105964,78745,121335,583391,47668,46429,1082416,41863,182138,67167,71033,45465,507705,849690,350538,211662,97652,21572,237302,83382,4878,646424,83084,4100,211414,219098,181333,154255,465084,455946,410211,309164,157757,435963,287853,724473,126582,442874,473103,207136,405141,34099,157592,105531,205622,888397,280429,157798,358748,70382,353148,196161,159385,147210,223084,126688,70858,32648,55152,255209,232257,883293,277856,152912,31724,164031,19212,460278,170217,103274,10279,119305,125781,28993,351984,426512,49803,41450,86142,148449,383171,1166727,78361,86085,499319,350990,269853,35681,454687,153550,322647,554606,15819,522365,832756,406942,129620,955217,194685,76365,104710,1451869,686359,138587,951014,163058,31631,406250,127686,289419,310474,338299,292060,70009,7077,1016101,13340,540157,156371,343427,439121,43474,506594,386,101535,346923,131016,542162,745311,51400,29445)
在R中成立x变量以记录序号,其代码如下:
x=c(1:140)
timediff的漫衍图如图1所示:
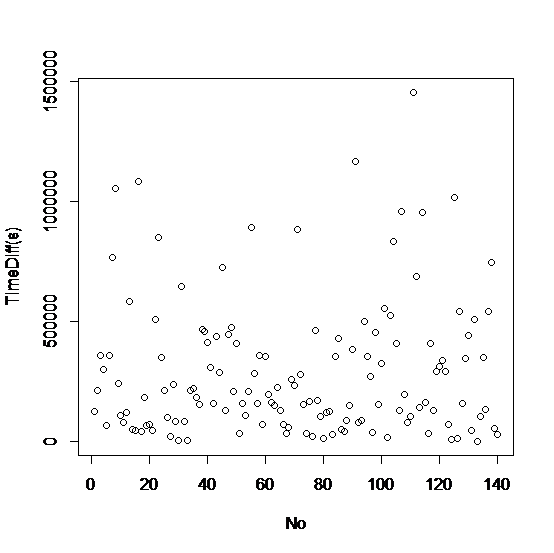 图1
图1
画图代码如下:
plot(timediff,xlab=”No”,ylab=”TimeDiff(s)”)
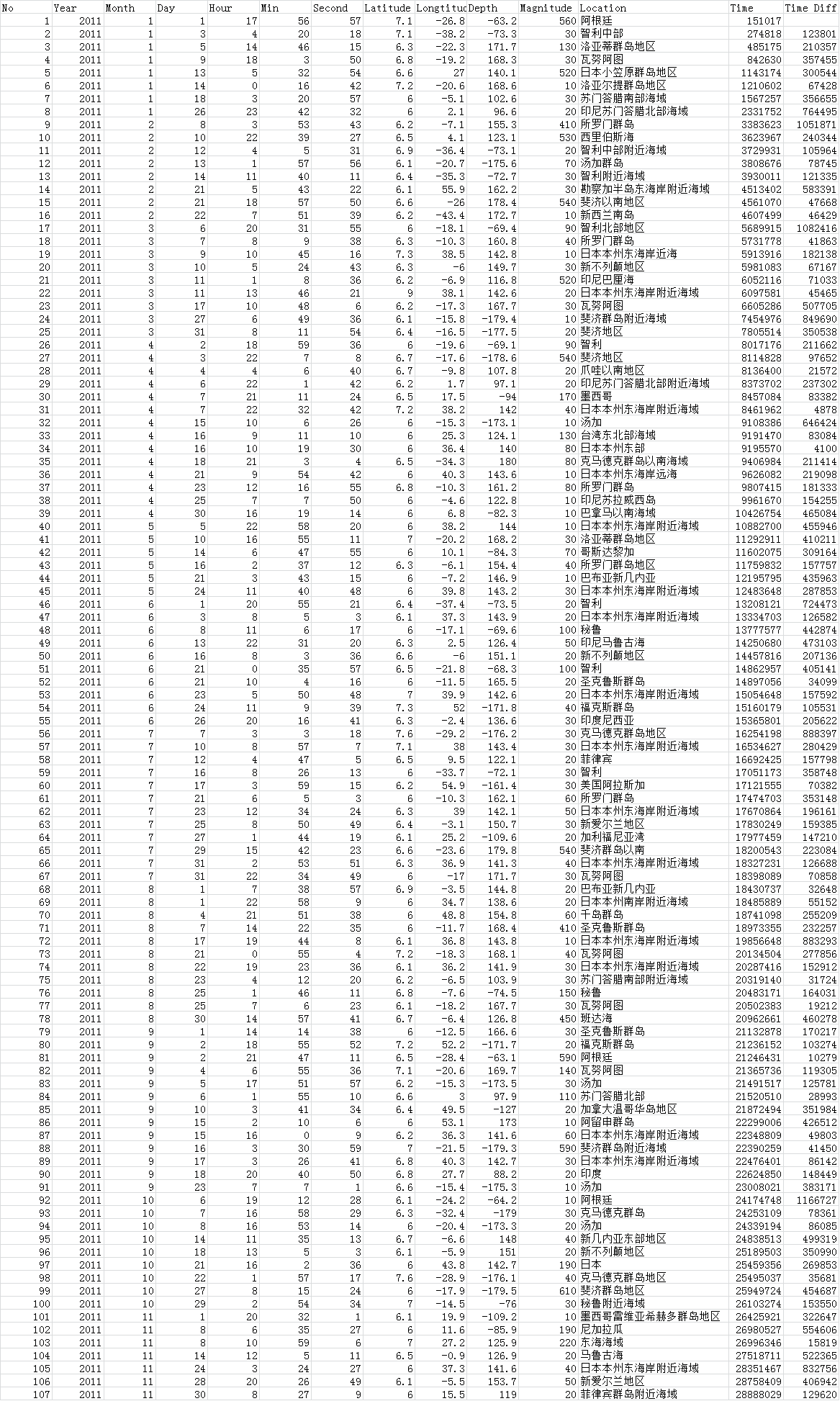
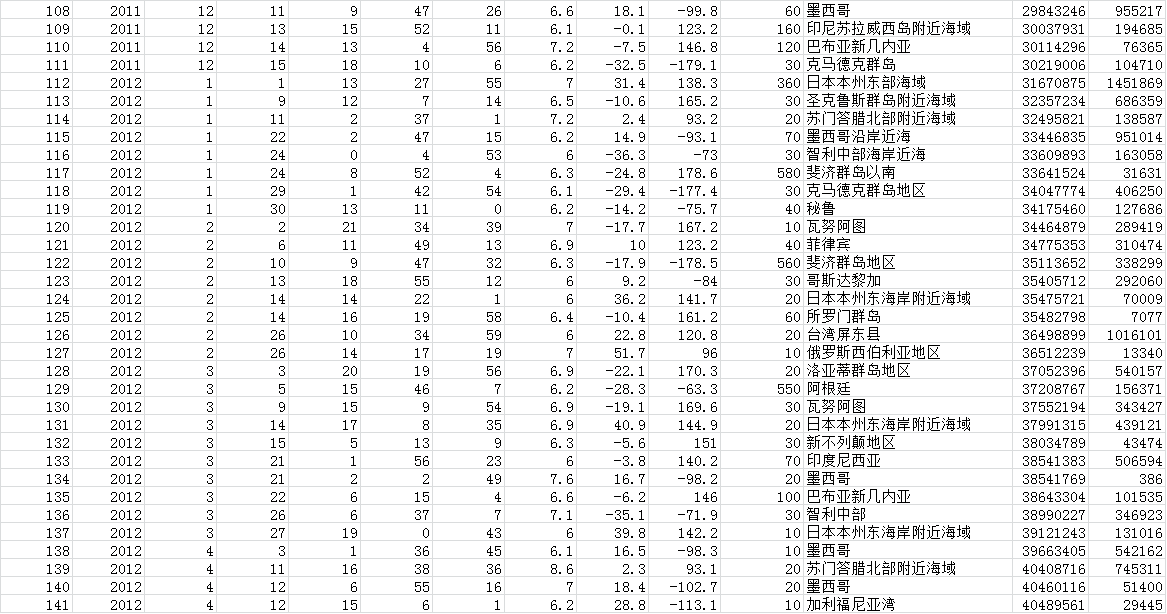
表1
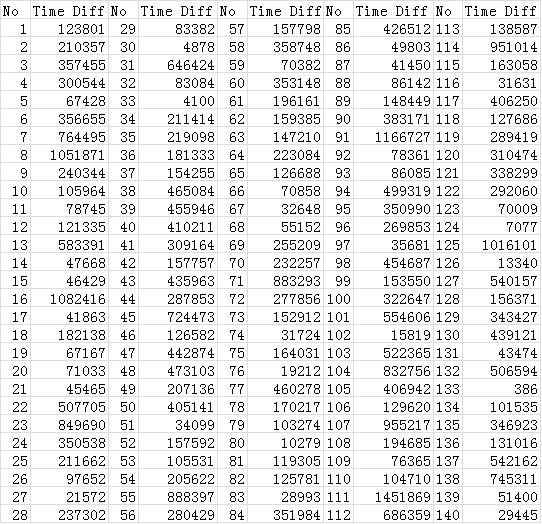
表2
二. 线性回归阐明:
1. 在R中别离成立x与timediff的一次、二次、三次以及四次的一元线性回归模子。其代码别离如下:
lm1=lm(timediff~1+x)
lm2=lm(timediff~1+x+I(x^2))
lm3=lm(timediff~1+x+I(x^2)+I(x^3))
lm4=lm(timediff~1+x+I(x^2)+I(x^3)+I(x^4))
各线性回归模子的详细信息别离如下:
> lm1
Call:
lm(formula = timediff ~ 1 + x)
Coefficients:
(Intercept) x
262461.8 364.1
_______________________________________________________________________
> lm2
Call:
lm(formula = timediff ~ 1 + x + I(x^2))
Coefficients:
(Intercept) x I(x^2)
303243.26 -1359.04 12.22
_______________________________________________________________________
> lm3
Call:
lm(formula = timediff ~ 1 + x + I(x^2) + I(x^3))
Coefficients:
(Intercept) x I(x^2) I(x^3)
3.737e+05 -7.255e+03 1.164e+02 -4.925e-01
_______________________________________________________________________
> lm4
Call:
lm(formula = timediff ~ 1 + x + I(x^2) + I(x^3) + I(x^4))
Coefficients:
(Intercept) x I(x^2) I(x^3) I(x^4)
2.686e+05 7.202e+03 -3.412e+02 4.543e+00 -1.786e-02
2. 操作summary()函数对线性回归模子举办阐明,其功效别离如下:
> summary(lm1)
Call:
lm(formula = timediff ~ 1 + x)
Residuals:
Min 1Q Median 3Q Max
-310504 -198032 -87695 110804 1148990
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 262461.8 47610.4 5.513 1.68e-07 ***
x 364.1 585.9 0.621 0.535
—
Signif. codes: 0‘***’ 0.001‘**’ 0.01‘*’ 0.05‘.’ 0.1‘ ’ 1
Residual standard error: 280200 on 138 degrees of freedom
Multiple R-squared: 0.002791, Adjusted R-squared: -0.004435
F-statistic: 0.3862 on 1 and 138 DF, p-value: 0.5353
> summary(lm2)
Call:
lm(formula = timediff ~ 1 + x + I(x^2))
Residuals:
Min 1Q Median 3Q Max
-338283 -196579 -89520 107429 1148904
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 303243.26 72173.83 4.202 4.75e-05 ***
x -1359.04 2363.19 -0.575 0.566
I(x^2) 12.22 16.24 0.753 0.453
—
Signif. codes: 0‘***’ 0.001‘**’ 0.01‘*’ 0.05‘.’ 0.1‘ ’ 1
Residual standard error: 280600 on 137 degrees of freedom
Multiple R-squared: 0.006898, Adjusted R-squared: -0.007599
F-statistic: 0.4758 on 2 and 137 DF, p-value: 0.6224
> summary(lm3)
Call:
lm(formula = timediff ~ 1 + x + I(x^2) + I(x^3))
Residuals:
Min 1Q Median 3Q Max
-317595 -206547 -78641 113669 1122985
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3.737e+05 9.740e+04 3.837 0.00019 ***
x -7.255e+03 5.961e+03 -1.217 0.22570
I(x^2) 1.164e+02 9.805e+01 1.187 0.23731
I(x^3) -4.925e-01 4.572e-01 -1.077 0.28330
—
Signif. codes: 0‘***’ 0.001‘**’ 0.01‘*’ 0.05‘.’ 0.1‘ ’ 1
Residual standard error: 280400 on 136 degrees of freedom
Multiple R-squared: 0.0153, Adjusted R-squared: -0.006421
F-statistic: 0.7044 on 3 and 136 DF, p-value: 0.551
> summary(lm4)
Call:
lm(formula = timediff ~ 1 + x + I(x^2) + I(x^3) + I(x^4))
Residuals:
Min 1Q Median 3Q Max
-349192 -200767 -71243 128635 1084767
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 2.686e+05 1.234e+05 2.177 0.0312 *
x 7.202e+03 1.203e+04 0.599 0.5504
I(x^2) -3.412e+02 3.452e+02 -0.988 0.3248
I(x^3) 4.543e+00 3.673e+00 1.237 0.2182
I(x^4) -1.786e-02 1.292e-02 -1.382 0.1693
—
Signif. codes: 0‘***’ 0.001‘**’ 0.01‘*’ 0.05‘.’ 0.1‘ ’ 1
Residual standard error: 279500 on 135 degrees of freedom
Multiple R-squared: 0.02903, Adjusted R-squared: 0.0002649
F-statistic: 1.009 on 4 and 135 DF, p-value: 0.4051
由于一元四次线性回归方程模子的显著性一般,而其他三个模子的显著性较好,故下文只接头一次、二次以及三次的一元线性回归方程模子。
3. 画图。绘制一次、二次以及三次的一元线性回归方程模子的图像,别离如图2、图3、图4所示:
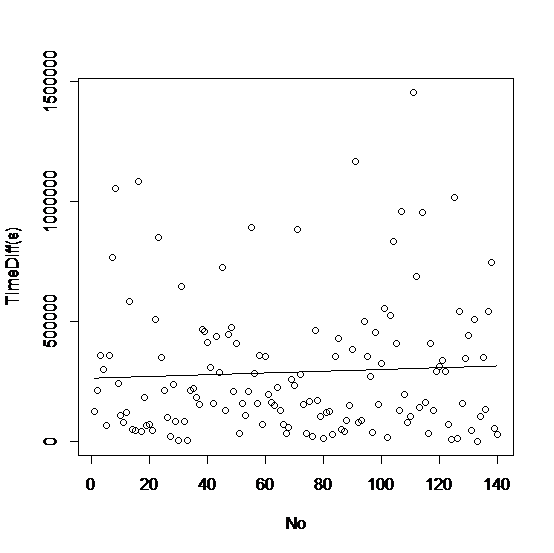 图2
图2
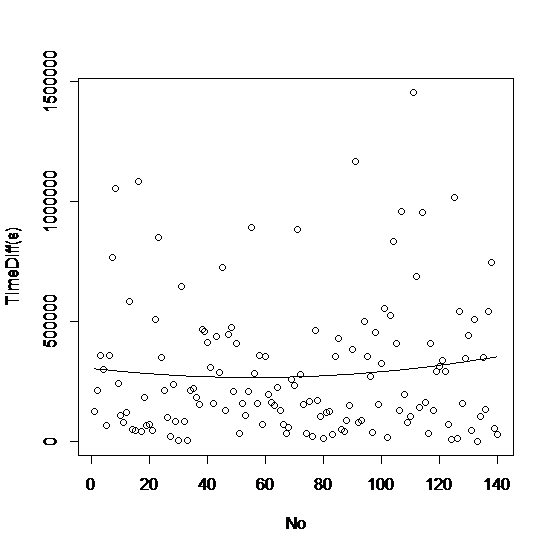 图3
图3
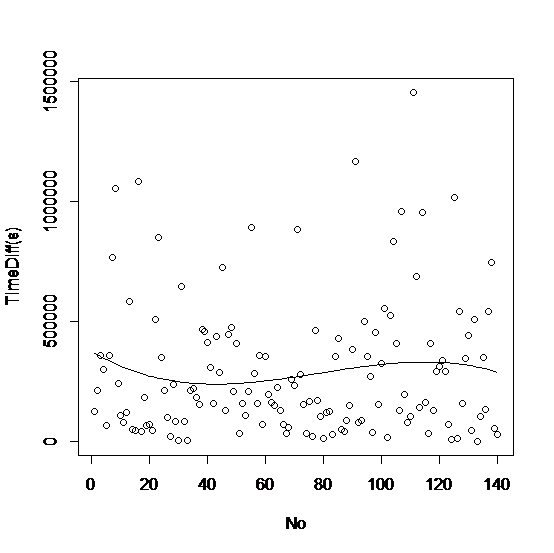 图4
图4
假设地球进入了地动高发期,即任一次大地动与其之前产生的一次大地动的时距离断(即Time Diff的值)逐渐减小,即模子所对应的函数在x=140四周为减函数。那么,从以上三幅图像易知,只有图4,即三次一元线性回归方程模子的图像与假设相符。故,下文的阐明将只对三次一元线性回归方程模子举办。
三. 预测以及阐明:
1. 预测:
操作predict()函数对下一次大地动产生的时间经行预测,其代码如下:
predict(lm3,pre,interval=”prediction”,level=0.6④)
其功效如下:
fit lwr upr
284078.4 33439.31 534717.4
2. 阐明:
由预测功效可知,在2012年4月12日15:06:01 产生在加利福尼亚湾的里氏6.2级地动之后约284078.4秒,即约莫79小时之后(约莫为2012年4月15日7点),将会在环太平洋地动带的某地再次产生震级大于里氏6.0级的地动。不外事实到底如何,看来照旧需要时间的检讨。
跋文
本次尝试的主要操纵部门已告一段落。可是有趣的是,在本文尚未完稿时,重新闻获悉,在2012年4月15号6时05分,瓦努阿图(太平洋岛国)产生里氏6.5级地动⑤。不外,我并不认为这代表着本次尝试的乐成,因为对付地动的预测并不是一件简朴的事。何况地动产生的原因到今朝为止人不被人类所相识,精确的预测地动不行能是一件简朴的事。需要考的相关因素也不会只有时间、震级与地动带的简朴因素,还应包罗震源深度,震时气候,甚至太阳黑子勾当⑥等许多其他因素。因此,本文旨在用所学过的根基常识对现实世界举办探讨的实验,并不期望可以获得什么惊人的结论。所做之尝试以及所作之文,由于本领有限,如有不敷,但愿可以获得各人的指正以及辅佐。
2012年4月15日下午
_______________________________________________________________________________
注释:
① :本文所有时间均以北京时间为准。
② :相关新闻网址:http://news.xinhuanet.com/world/2012-04/12/c_122970102.htm
③ :数据来历网站:http://www.ceic.ac.cn/
④ :为担保置信区间在公道范畴内,利用了较量低的置信程度。
⑤ :相关新闻网址:http://news.qq.com/a/20120415/000330.htm
⑥ :相关新闻网址:http://www.people.com.cn/GB/paper447/2576/382835.html
最后,爱特我亲爱的队友们~~We got it! @litian1045 @suan0919
