IEOR 3609:Advanced Optimization
Nonlinear and Convex optimization
Final Exam: IEOR 3609
高级优化考试代写 Problem 2. (20 points)A university wants to schedule all exams on a single day using minimum number of rooms possible.
Please read the following instructions carefully before beginning your exam.
Submission Instructions.
- The exam contains five problems. (Total = 100 points). Exam duration: 2 hours.
- Please write your name and UNI clearly on the first page of your submission. Also, please write your UNI on top of every page of your submission.
- You do not need to print or copy the questions in your submission. Just submit your solutions, with clearly marked problem numbers.
- Submit on gradescope. Please take a clear photo or scan of your exam and upload it on the gradescope within 15 minutes of exam close time (i.e., by 10:15pm EST). The upload process is similar to homework submission. If you are having difficulty accessing gradescope, email a copy to the instructor and TA with subject line ”IEOR 3609 exam” in order to timestamp it.
Queries during exam 高级优化考试代写
- All the problems should be self-explanatory. Any student queries asking for further explanation of a problem will not be entertained, as it is not fair to other students who did not receive the additional explanation. If you feel that a problem statement is ambiguous, provide your interpretation of the problem, and answer it according to that interpretation.
- If there are any pressing queries during the exam, go to the zoom meeting for instructor office hours. Only one person will be admitted at a time, so you may have to wait in the waiting room.
- DO NOT post queries publicly on Piazza or any discussion forum during the exam.
Academic Integrity 高级优化考试代写
- The exam is open book. However, you must take the exam completely on your own. You should not show or discuss your exam with anyone (in-person or online or through chat/email).
- You may use a calculator if needed, although the exam can be solved without using a calculator. No other software (like Gurobi or Matlab etc.) and no online applications should be used during the exam.
- DO NOT post or share the exam or your solutions online during or after the exam. Any violations of the above policies will be considered academic dishonesty and violation of honor code, and can be subject to disciplinary action.
Problem 1. (20 points) 高级优化考试代写
Consider the following problem:
Maximize 2x1 + 3x2
s. t. x1+ x2 ≤ 11
− 2x1 + 3x2 ≤ 1
x1 − x2 ≤ 3
x2 ≥ 0,
x2 integer,
x1 ∈ {0, 1, 2, 6, 8}
(a) Reformulate the above problem as an equivalent Integer Program (IP). (Note that in the current formulation stated above, the last constraint is not an IP constraint.)
(b) State which of the following are valid inequalities for this problem. Justify.
(i) −x2 + x1 ≤ 0
(ii) x1 ≤ 3
(iii) x1 ≤ 9
Problem 2. (20 points)
A university wants to schedule all exams on a single day using minimum number of rooms possible. There are 100 rooms available. Each room is available for 12 hours in a day. There are a total of 40 exams of three different types to be scheduled:

(a) Formulate the Master Problem (MP). Clearly describe the set of all possible columns in MP.
(b) As a starting point, consider the three configurations each with maximum number of exams of a single type that can fit in a day. That is, the configurations with twelve 1-hour exam, with six 2-hour exams, and with four 3-hour exams, respectively. Formulate the restricted masters problem (RMP) using only these three columns.
(c) Compute the optimal solution for the RMP formulated in part (b).
(d) Formulate the pricing problem to check whether all reduced costs are non-negative and the solution computed in part (c) is an optimal solution for the master problem.
(e) Use the pricing problem formulated in part (d) to suggest a column that has negative reduced cost, and therefore can be added to the RMP in the next iteration.
Problem 3. (20 points) 高级优化考试代写
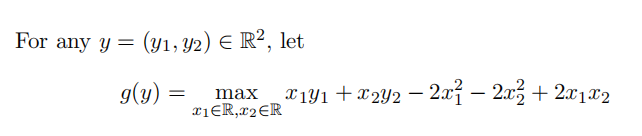
(a) Prove or disprove: g(y) is a convex function in y.
(b) Argue that for any given y, the above maximization problem (in x) is a convex optimization problem.
(c) Use optimality conditions for unconstrained convex optimization to eliminate x and express g(y) in a form that involves only y1, y2 (and not x1, x2).
Problem 4. (20 points)
Consider the following convex optimization problem.
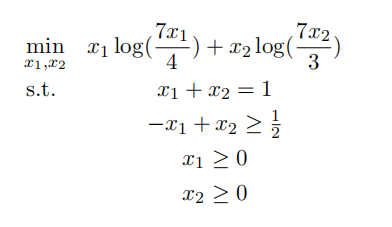
(a) Formulate the dual problem. Simplify the dual objective to express the dual in a form which involves only the dual variables (but not x1, x2).
(b) Use KKT conditions to construct an optimal solution to the primal and the dual problem. Hint: In the optimal solution, x1 > 0, and x2 > 0.
Problem 5. (20 points) 高级优化考试代写
Argue that the following is a convex constrained convex optimization problem. Write down the KKT conditions for optimality. Use KKT conditions to find an optimal solution. Show your work.
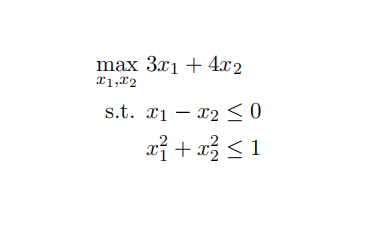

更多代写:Java代写 托福代考 英国Geography地理学代写 澳洲论文essay代写 ib课程论文代写 田纳西大学代写
