Exam 1
高等微积分考试代写 You have an hour and 15 minutes for this test. Please show all reasoning; you may not get credit for answers which are not justified.
You have an hour and 15 minutes for this test. Please show all reasoning; you may not get credit for answers which are not justified. You may assume all results which have been given in class, in the book or in the homework. Since some problems are more difficult than others, please pace yourself so that you can try all of them. All problems have equal point value. Please do not use calculators. Good luck!
Points
(15)1.(a)For DB2 + C2 + D$ – 1 = 0, compute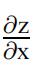
and 
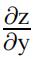in terms of x,y,and z. 高等微积分考试代写
(b) Write down an expression for dz in terms of dx and dy
(15) 2. Let 0 be a function from 
to 
given by
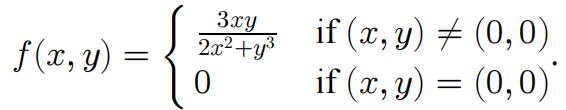
Determine whether the limit 
exists,and find its value if it does.Justify your answer either way.
(15) 3. LetZ1=v1v2,z2＝v1+v2,v1＝u21+u2,v2＝u22 From this find the matrix 
as a product of two matrices, where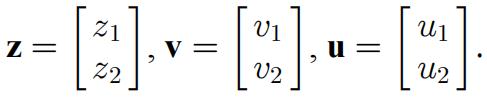 
Compute the value of this matrix at the values u1=1,u2=2.
(15) 4.Compute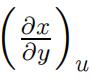 
if x2u+v＝0 and yv＋xu＝2 高等微积分考试代写
(20) 5.Consider the relationships x2+yu+xv＝5 and xv+y2u. Let dx ＝
and
where dx ,dy,du,dv are the differentials of the variables.
(a)Compute
if x,y are viewed as functions of u,v.
(b)At given fixed values for x=1,y=2,u=1,v=2 satisfying these relationships,
consider a matrix E such that dx = Adu. Find the top row (first 2 entries) of A.
(20) 6. Assume that the variables x,y,z, and w are related by a pair of equations. Assume that if we were to solve for z and w in terms of x and y, the partial derivatives would solve the equation 高等微积分考试代写
zx = wy.
Prove then that if we were to solve instead for z and x in terms of w and y, we would have
zw = – xy
更多代写：商科文学assignment代写 雅思代考 商科网课代修代上 商业essay论文代写 商业论文写作方法指导 大学功课代做价格
