INSY 3400
Stochastic Operations Research
随机运筹学代写 Assignment overview. The purpose of this assignment is to illustrate how class topics can relate to principles of other sciences.
Programming Assignment 2 随机运筹学代写
Due date: Monday, December 2nd, by the end of the day (11:59pm).
Late submissions: a penalty of 20% of the grade per day will be applied to late submissions
You are free to use a programming language of your choice, but I would encourage you to use Python. If you are not in INSY 3010, then use the same language that you have used for assignment 1.
Assignment overview. The purpose of this assignment is to illustrate how class topics can relate to principles of other sciences. Specifically, we will introduce a model for chemical reactions, and then use continuous Markov chain ideas to make conclusions.

Underlying model: 随机运筹学代写
The description below is based on http://people.uleth.ca/˜roussel/ C4000foundations/slides/22CME_I.pdf. Consider a volume occupied by molecules of three chemicals: A, B and C. Denote as nA, nB and nC the number of molecules of each. The three chemicals can react according to the following equation:
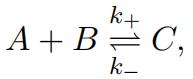
i.e., one molecule of A and one molecule of B can react to produce 1 molecule of C, while 1 molecule of C can decay into 1 molecule of A and one of B. k+and k− are values representing how often the re- actions Chemical master equation can then be used to describe the system evolution https://en.wikipedia.org/wiki/Master_equation. The reaction propensities can be estimated given the number of molecules. Propensity for the forward reaction is a+ = k+nAnB and for the backward re- action is a− = k−nC (intuitively, the rate at which a reaction happens is proportional to how often the molecules collide).
We will model this system as a birth-and-death (BD) process.
The states will represent the number of molecules of each chemical present. It is then natural to interpret the reaction propensities as the transition rates in the BD process. For the simple reaction above, from state (nA, nB, nC ) the system can transition to state (nA 1, nB 1, nC + 1) if the forward reaction happens, or to state (nA + 1, nB + 1, nC 1) for the backward reaction. So for example, if initially you have 4 A molecules and 3 B, then the system canbe in states: (4, 3, 0), (3, 2, 1), (2, 1, 2), (1, 0, 3), and, for instance, transition rate from (4, 3, 0) to (3, 2, 1) is 4 3 k+ = 12k+.
Your task is to determine the equilibrium state distribution, i.e., the long-run proportions for the BD process.
Directions:
1.Assume that initially you only have NAmolecules of A and NB of B (and no C molecules). Obtain your values for k+, k−, NA, NB:
for k+: https://www.wolframalpha.com/input/?i=random+number+between+0. 1+and+5
for k−: https://www.wolframalpha.com/input/?i=random+number+between+0. 1+and+5
for NA: https://www.wolframalpha.com/input/?i=random+number+between+ 20+and+200
2.Your BD process will have total of N = min NA, NBstates: (NA, NB, 0), (NA 1, NB 1, 1) . . ., with transition rates according to the reaction To be consistent with the notation used inclass, let’s number the states as 0, 1, . . . , N , so that for example, state 3 corresponds to state (NA − 3, NB −3, 3). Then, one can determine that the transition rates “forward” λn = k+(NA −n)(NB −n), and “backward” transition rates are µn = k−n. 随机运筹学代写
3.Recall the solution for long-run proportions equations in BDprocesses:
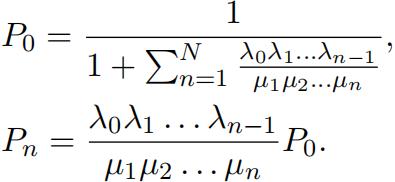
4.Writea code, to determine equilibrium Specifically, define a function, which takes values k+, k−, NA, NB as arguments and returns a list of values P0, P1, . . .
5.Find the average proportion of each chemical in the equilibrium.
Submission instructions. Submit your code and a brief report on Canvas. In the report clearly identify the values for the parameters that you used and values you obtained. The report should be in .pdf, .doc or .docx format. If you are using Python submit your .py file(s). Your code should have definition for the function for finding probabilities.

