MA 583 Final Exam
随机过程代考 Find a stationary distribution π = (π0, π1, ….) for this Markov Because this has infinity terms your answer should be a formula for πkin terms of k.
Instructions: 随机过程代考
- Upload a PDF of your exam solutions before 8:00 AM EDT August 14, 2020.
- Explain all of your steps.
- There is no need to simplify arithmetic (unless statedotherwise).
- You may refer to the textbook, recorded lectures, homework assign- ments, and lecture notes.
- You may not use any resources other than the textbook, recorded lec- tures, homework assignments, and lecture notes.
- You may not use any resources other than the textbook, recorded lec- tures, homework assignments, and lecture notes.
- You may not use a calculator or calculator website.
- You may not collaborate with anybody.
- Do not cheat.
1.(20points) Consider the success run Markov chain Xn on state space {0, 1, 2, 3, ….} with transition probabilities
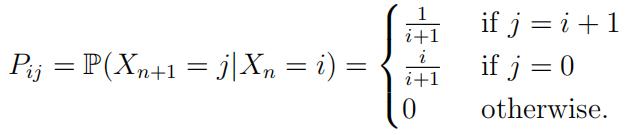
(a)Write rows 0,1,2,3 and 4 of P.
(b)Find a stationary distribution π = (π0, π1, ….) for this Markov Because this has infinity terms your answer should be a formula for πkin terms of k.
Show all of your work and explain each step. You will get a lot of partial credit if you leave a summation in your answer, but for full credit you should simplify the sum.
Hint: the Taylor series for ex 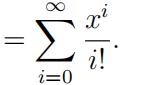
(c)Findthe period of state Show all of your work and explain each step.
2.(20 points) Let X(t) be a continuous time Markov chain with state space 0, 1, 2, 3, 4. 随机过程代考
Let Pij(t) = P(X(t) = j X(0) = i). Suppose that the infinitesimal generator of P (t) is the matrix
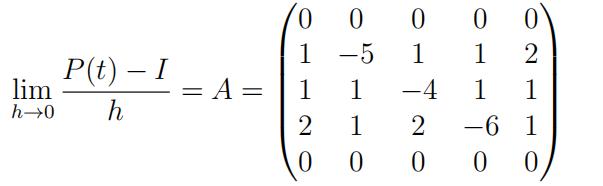
(a)Let τ = min t 0 : X(t) = X(0) be the time of the first jump. Calculate E(τ X(0) = 1). Show all of your work and explain each step.
(b)Let τ = min t 0 : X(t) = X(0) be the time of the first jump. Calculate P(X(τ ) = 2 X(0) = 3). Show all of your work and explain each step.
(c)Let T = min t 0 : X(t) = 0 or X(t) = 4 be the first time that the Markov chain enters state 0 or 4.Let
ui = P(X(T ) = 0|X(0) = i).
Using first step analysis, set up a system of linear equations for u1, u2, and u3. Explain all of the terms in your system but DO NOT SOLVE THE LINEAR SYSTEM. JUST SET IT UP AND EXPLAIN YOUR STEPS. 随机过程代考
(d)Assume that the initial distribution is
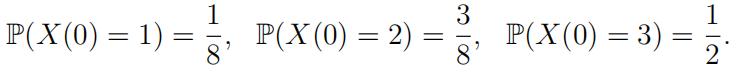
Find an expression for P(X(T ) = 0), where T is defined as in part (c). Write your answer in terms of the u1, u2, u3 from the previous part. DO NOT SOLVE FOR u1, u2, or u3. Show all of your work and explain each step.

3.(20points) Let X(t) be a Poisson process with parameter λ = Let Wi i = 1, 2, 3, … be the ith arrival time
Wi = min{t ≥ 0 : X(t) = i}.
(a)Calculate
P(X(4) = 3, X(2) = 3, and X(1) = 1).
Show all of your work and explain each step.
(b)Calculate
E(X(2)X(5)).
Show all of your work and explain each step.
(c)Calculate
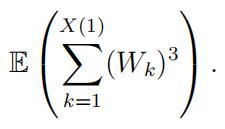
Show all of your work and explain each step.
4.LetXn be a reducible Markov chain on the state space 0, 1, 2, 3, 4, 5 with the transition matrix 随机过程代考

(a)Identifythe communicating classes of the Markov chain and clas- sify each class as recurrent or Explain your answer.
(b)Calculate
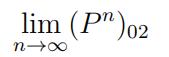
Your answer should be exact. Do not use a calculator and do not give a decimal approximation. Show all of your work and explain each step.
(c)Calculate
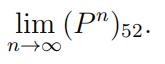
You answer should be exact. Do not use a calculator and do not give a decimal approximation. Show all of your work and explain each step.
5.Let X(t)= 4 3t + 2B(t) where B(t) is a standard Brownian motion with B(0) = 0. 随机过程代考
(a)Calculate
E(X(2)).
Show all of your work and explain each step.
(b)Calculate
E(X(2)X(1)).
Show all of your work and explain each step.
(c)Let τ = min{t ≥ 0 : X(t) = 0 or X(t) = 8}.Calculate
P(X(τ ) = 0).
Please cite formulas from the textbook or notes. Do not give a decimal approximation of your answer. Show all of your work and explain each step.]

