Problem Set代写 distance function代写 1-dimensional clustering代写

Problem Set 2

Problem Set代写 Due date: Wed, Nov 7, 2018 at 5:00pm. Submit a hard copy in the closed CS565 dropbox. Write every problem on a separate page

Due date: Wed, Nov 7, 2018 at 5:00pm. Submit a hard copy in the closed CS565 dropbox. Write every problem on a separate page, make sure your name is on each page and staple them together. Typed solutions are preferred but had writing is also accepted.

Exercise 1 (25 points): Problem Set代写

Consider a set of d-dimensional points X = {x₁, . . . , x_n} and distance function

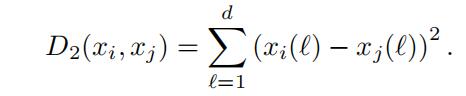
Show that the representative

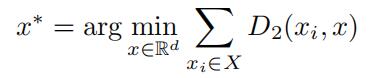
is the mean of the points in X. That is, for every A ∈ {1, . . . , d} x^∗(A) = ¹ Σn x_i(A). (10 points).

Consider a set of d-dimensional points X = {x₁, . . . , x_n} and distancefunction

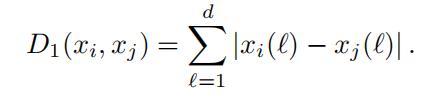
Show that the representative

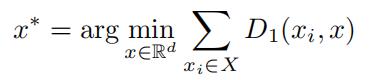
is the median of the points in X. That is, for every A 1, . . . , d x^∗(A) = median(x₁(A), . . . , x_n(A) . (15 points).

Exercise 2 (30 points):Problem Set代写

Consider the following 1-dimensional clustering problem: given a set of n 1- dimensional data points X = x₁, . . . , x_n and an integer k partition these points into clusters of size at least k such that if the resulting number of clusters is A

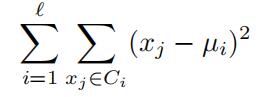
is minimized. In the above equation, C_i is the i-th cluster and µ_i is the representative of this cluster – in this case the mean of the data points in the cluster.

Designa polynomial-time algorithm for finding the optimal clustering C. (15 points)
If the running time of the algorithm you described above is linear then, you get 15 points. If the running time is more than linear, design a linear-time algorithm for the above problem. (15 points)Problem Set代写

Exercise 3 (30 points):

In this exercise you will devise an algorithm A that, given two degree sequences,generates a graph with corresponding degrees. That is, the input to A are two integer sequences d =

{d₁, d₂, . . . d_n1 } and q = {q₁, q₂, . . . q_n2 }. The output of A(d, q) is a bipartite graph tt(U, V, E), such that the number of nodes |U | = n₁, |V | = n₂ and the nodes in U have degrees d₁, d₂, . . . d_n1 and nodes in V have degrees q₁, q₂, . . . q_n2 .Problem Set代写

(tt is simple, that is, it has no multi-edges.)

First,give a necessary and sufficient condition on the sequences d and q that there exist such a (ex. There is clearly no graph for the sequences d and q, such that every i we have d_i = 1 and for every j we have q_j = 0.) Prove that the condition is necessary. You will prove that it is sufficient in part 3 of this problem. (7 points)

Definethe algorithm A and analyze its running (10 points)Problem Set代写
Provethatyour algorithm always terminates and, given that the condition in part 1 is fulfilled, always outputs a valid (8 points)
Algorithm A takes two sequences as an input. It is a natural question to ask, whether we can also devise an algorithm B that takes only one sequence as input and outputs a general (non-bipartite) graph with the given degree sequence as output? This problem is in fact harder to solve (though, it is still polynomial), and you are not asked to do that. However, give an example that shows that the same algorithmic approach as A does not always work for this case. (e.g. show a graph, such that givenits degree sequence, the single partite version of A would not find the corresponding ) (5 points)Problem Set代写

Exercise 4 (25 points):

Consider the edit distance between two labeled graphs tt₁ = (V, E₁) and tt₂ = (V, E₂) with the same set of nodes to be the number of edges in E₁ that are not in E₂ plus the number of edges in E₂ that are not in E₁. That is,

∆(tt₁, tt₂) = |E₁ \ E₂| + |E₂ \ E₁|.

Prove that ∆() is a metric. (10points)Problem Set代写

Given a set of graphs tt₁, tt₂, . . . , tt_n consisting of n graphs all sharing the same set of labeled nodes design an algorithm for finding the centroid of the set of clusters, when distance ∆ is used as a distance function between graphs. (15 points)

合作平台：天才代写幽灵代写写手招聘 Essay代写