Problem 2
金融经济课业代写 Question 1 (Equilibrium with certainty)Consider a one-period economy with two dates (t = 0 and t = 1) and certainty. The utility for each agent is:
Question 1 (Equilibrium with certainty)
Consider a one-period economy with two dates (t = 0 and t = 1) and certainty. The utility for each agent is:
Ui(Cit) = ln(ci0) + ρ2 ln(ci1),
Where ρ is the so-called rate of intertemporal consumption. Agents’ endowments are denoted with (ei0, ei1), i = 1,2, … ,I. Define Et as the sum of the agents’ endowment at t, and assume that the economy grows at the rate g, i.e., Et/Et-1 = 1 + g. There are personal loans; that is, agents can lend and borrow to each other at the interest rate r.
a) Given the interest rate r, find the optimal borrowing and do comparative static analysis (that is show how the optimal borrowing changes as each of the parameters of the economy change, keeping the rest constant (ceteris paribus)).
b) Find the equilibrium interest rate in the economy. How does it relate to ρand g?
c) Show that if the loan market clears, the two good markets also automatically clear.
Question 2 (Equilibrium with uncertainty) 金融经济课业代写
Consider a one-period model with S = 2 and two agents I = 2. The utility function for each one is:
Ui(c) = ln(ci0) + βπln(ciG) + α(1 − π)ln(ciB),
where G stands for the Good state of the world, while B for the Bad one. Assume that Arrow securities can be traded.
Suppose that the endowments of each agent i is given by: (ei0, eiG, eiB).
a) What are the Arrow securities prices in this economy with two agents? Express the Arrow securities prices as functions of (ei0, eiG, eiB, β, α,π)? Interpret your results.
b) Given the following specific endowments: Agent 1: (5,5,2); Agent2: (5,3,4), and assuming that β = 0.25, α = 0.5, π = 0.8. 金融经济课业代写
i) Find the optimal consumption of each agent.
ii) Is this allocation Pareto superior (everybody is better off) to the autarky allocation?
c) Find the interest rate of this economy.
d) Given the following alternative endowments: Agent 1: (7, 5, 2); Agent 2: (7, 3, 4) find the risk free interest rate in this economy.
e) Given the next payoffs:
| States | Good | Bad |
| Project | 48 | 40 |
i. Find out the expected present value of the project.
ii. Find out the prices at t=0, using the Arrow Securities you found in d).
iii. Find the risk adjusted interest rate (or, WACC) of the project.
Question 3 (Arbitrage and Equilibrium pricing) 金融经济课业代写
You live in an economy with two dates (t =0, 1). At t = 1, there are two states: growth or recession. Security markets meet at t = 0.
a) Suppose that the two Arrow securities (AS), whose prices are 0.4 (AS-growth) and 0.5 (AS-recession) respectively, can be traded. There are two stocks in the economy, and their payoffs are shown in the following table.
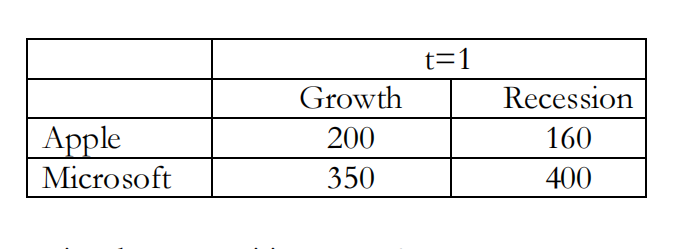
i. Find the share price these securities at t = 0.
ii. Suppose Apple trades for 166 at t = 0. Can you find an arbitrage strategy? If yes, what is the profit from this strategy?
iii. What is the interest rate of this economy?
b) In part a) we assumed we knew the prices of Arrow securities. Suppose that the arrow securities are traded and their prices are not known. Instead, the economy has ? Each agent is endowed with (ei0, eiG, eiR). In the growth state, the total endowments will increase by 30%; however, the total endowments will decline by 8% in the recession state. Their utility function is given by
ui(cis) = ln(ci0) + 0.52ln(ciG) + 0.46ln(ciB).
i. Can you find the prices of the Arrow securities in this economy?
ii. Are the Arrow securities prices endogenous or exogenous here?
c) Now, we assume the agents can trade Apple and Microsoft but not the Arrow Securities. We keep all other economic setting the same as part b). Use the payoffs shown in the table of part a).
i. Can you find the prices of Apple and Microsoft in the economy? Are they the same as using the prices of Arrow securities?
ii. Are the prices of securities endogenous or exogenous?
Question 4 (Term structure) 金融经济课业代写
Imagine you observe the following prices for the zero-coupon bonds issued by “riskless” US Treasury and with a face value 1000.
| Maturity | Zero-coupon Bond Price today |
| 1 | 988.78 |
| 2 | 980.56 |
| 3 | 976.78 |
| 4 | 934.79 |
| 5 | 862.40 |
a) Obtain the term structure of interest rates, i.e., the sequence of (r01, r02, r03, r04, r05). Draw the yield curve.
b) Assume the forward interest rate r13=1.5%. Is there an arbitrage opportunity? If yes, please find one arbitrage opportunity.
c) A US national bank issues two types of bonds, with a principal of 10,000. Find the no arbitrage prices of each bond.
i. The first is a 3-year bond with coupon 2% with 100% repayment of the principal;
ii. The second is a perpetual bond with coupon of 1.5%. Assuming, for simplicity, that the yield curve is flat after year 3 at the rate r03.

