金融模拟方法代考 Simulation Methods代写

Simulation Methods for Finance EXAM

金融模拟方法代考 Let Xi, i = 1, 2,. . ., be independent and identically distributed Poisson random  varpiables  with  parameter  λ >  0.

1.(a)[5 marks] Let X be a Poisson random variable with parameter L > 0.    金融模拟方法代考

Assume one knows how to generate standard uniform  Design an algorithm to generate random variable X.

(b)[10marks] Let X_i, i = 1, 2,. . ., be independent and identically distributed Poisson random  varpiables  with  parameter  λ >  0. Define  S_n =  X₁ + · · + X_n and  Z_n =(S_n — nλ)/   nλ.  Find the characteristic function of Z_n and its limit as n tends to ∞,then conclude that Z_n converges in distribution to a standard normal random variable.

(c)[10 marks] Continue (b). Prove that

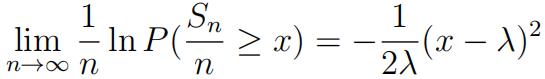
for x > λ. (Hint.  You may use the following fact without proof that lim_x!1 ^xØ(—x) = 1, where 0(x) is the cumulative distribution function of a standard normal variable and Ø(x) = Φ⁰(x).)

2.(a)[7 marks] Assume that random variables X and Y have a joint probability density function

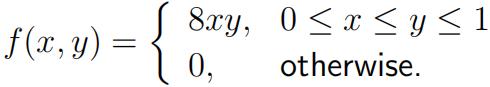
Let U = X/Y and V = Y . Prove that U and V are independent random variables and find their probability density functions. Furthermore, let U₁ and U₂ be two independent samples from standard uniform distribution U[0, 1]. Use U₁ and U₂ to construct X and Y such that (X, Y ) is a sample with pdf f.    金融模拟方法代考

(b)[9marks] Let X be a nonnegative random variable with

Let Y be a standard exponential variable with pdf g(x) = exp(—x). Find the maximum

c such that

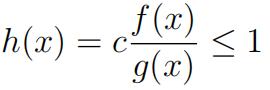
for all x ≤ 0 and design an acceptance-rejection algorithm to generate variate X by using variate Y . Explain why we want to choose c as large as possible.

(c)[9marks] Let X be a Poisson random variable with parameter λ. Find the cumulant generating  function  of  X,  defined  by  Γ(θ)   =   ln E[eθ^X],  and  its  Fenchel-Legendretransform, defined by F*(x) = supθ2R(θx — Γ(θ)).  Furthermore, show Γ^*(x)  is strictly positive for all x except at one point and find that point.

3.Let(Ω, F,P)  be a probability space, equipped with a filtration (F_t)_t≤0.    金融模拟方法代考

Let (W_t)_t≤0 be astandard Brownian motion and (N_t)_t≤0 be a Poisson process with intensity L, both W and N are adapted to the filtration (F_t)_t≤0 and are independent of each other.

(a)[3marks] Let X satisfy stochastic di↵erential equation (SDE)

dX_t = adt + bX_tdW_t, 0  t  T, (1)

with X₀ = x, where a, b are constants. Assume the Euler scheme is used to solve SDE (1)Write out the correspondingalgorithm.

(b)[5 marks] Continue (a). Solve SDE (1) and find the solutionX.

(c)[3marks] Find the quadratic variation of the process W_t + N_t for t ≤ 0.

(d)[4marks] Assume one knows how to generate independent standard uniform  Explain how to generate a sample path of (N_t)_t≤0.

(e)[6marks] Prove that ^Nt  tends to L almost surely as t tends to 1.

(f)[4marks] Prove that process (N_t — Lt)² — Lt, t ≤ 0, is a martingale.

4.Let(Ω, F,P)  be a probability space, equipped with a filtration (F_t)_t≤0.    金融模拟方法代考

Let (W_t)_t≤0 be a standard Brownian motion, adapted to the filtration (F_t)_t≤0. Assume the risky asset S satisfies the SDE

dS_t = rS_tdt + oS_tdW_t, t ≤ 0

with S₀ = S, where r > 0 is the riskless interest rate and o > 0 is the volatility. Assume one can generate independent standard normal variables.

(a)[8marks] The payo↵ of an Asian put option at time T is given by (K — A_T)⁺, where

K > 0 is a constant and  is the average of asset prices S_t with t_i = ih,i = 1, 2,. .., m, and h = T/m. The Asian put price at time 0 is given by

V (S) = E[e^—rT(K — A_T)⁺].    金融模拟方法代考

Describe the simulation method to compute the value V (S) and the pathwise derivative method to compute its delta V ^‘(S).

(b)[8marks] The payo↵ of a digital option at time T is given by A_T = 1_ST ≤K, where K > 0 is a constant, S_T is the asset price at time T , and 1_B is an indicator that equals 1 if the event B happens and 0  The digital option price at time 0 is given by

V (S) = E[e^—rTA_T].

Describe the simulation method to compute the value V (S) and the likelihood ratio method to compute its delta V ^‘(S).

(c)[9marks] The value of an American put option at time 0 with expiry time T and strike price K is given by

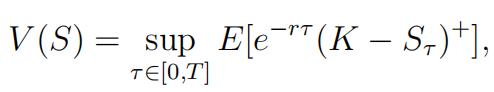
where Τ is any stopping time in the time interval [0,T]. Describe the Longstaff and Schwartz regression method to compute V (S) with basis functions 1, x, x², x³.

 

更多代写：Statistics统计学代写  多邻国代考  Psychology心理学代写  Statement of Purpose代写  Results代写  代写代考安全吗

合作平台：essay代写 论文代写 写手招聘 英国留学生代写