金融数学代考 Economics代写 Econ 659代写

Econ 659, Winter 2022, Practice Problems 1

金融数学代考 Inparts (a) through (c) below, use Ito’s lemma to write the stochastic process y in the standard form dy = a(y, t)dt + b(y, t)dz.

1.Inparts (a) through (c) below, use Ito’s lemma to write the stochastic process y in the standard form dy = a(y, t)dt + b(y, t)dz. dz is a standard Wiener

(a)y =z²

(b)y= 2 + t + e^z

(c)y= ¹ x² and dx = η(x¯ − x)dt + σxdz where x¯, η and σ are constants.   金融数学代考

2.Use Ito’s lemma to showthat:    金融数学代考

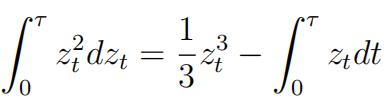(1)

where dz_t is a standard Wiener process.

3.Suppose you are participating in a game in which you roll a six sided dice and will winthe value of whatever you roll times  You can roll up to 4 times. After each roll you can either accept the prize given by that roll, or reject it and roll again. Let V_i denote the expected value of your prize assuming you act optimally over the entire game from roll i and onward. Let W_i denote the number on the dice for the ith roll. Find the expected value of your prize, V₁, as well as V₂, V₃, and V₄. Determine the optimal strategy.

4.Consider a 1 year futures contract on an investment  asset that provides no income and has no convenience yield.   金融数学代考

(An investment asset is one that is held by a significant number of individuals as an investment, rather than for consumption. Gold and silver would be ) It costs $10 to store the asset for a year, payable at the beginning of the year.  The current spot price of the asset is $200 and the risk free interest rate   is 5%.

(a)Suppose the futures price is $ Demonstrate whether this is an equilibrium price.If not, explain how an arbitrager can make a risk free profit.   金融数学代考

(b)Suppose the futures price is $ Demonstrate whether this is an equilibrium price.If not, explain how an arbitrager can make a risk free profit.

(c)Discuss how the actions of arbitrageurs would be expected to cause prices to adjust to an equilibrium level.

5.An individual enters into a one year long forward contract on an investment  asset with no income or storage cost when the asset’s spot price is $50 and the risk free rate of interest is 5% per annum (with continuouscompounding).    金融数学代考

(a)What are the forward price and the initial value of the forwardcontract?

(b)Six months later, the price of the stock is $55 and the risk free rate is still 5%. What are the forward price and the value of the forward contract? Explain why these have changed.  金融数学代考

6.Inclass we derived the relationship between the spot and futures price of an  For commodities, that relationship is f_t = S_te^(r+u−δ)τ where f_t is the futures price at time t, S_t is the spot price, u is the storage cost, δ is the convenience yield and τ is the time to maturity of the forward contract. We now assume that δ includes storage costs, so we drop u and are left with

ft  = Ste^(r−δ)τ. (2)

Recall that r δ is the risk adjusted drift rate of the asset’s price in the risk neutral world.

Suppose the asset S has a constant expected growth rate as in a GBM process: dS = αSdt + σSdz. Then we know that the expected value of S in the risk neutral world is given by:

E(S_τ ) = S_te^(r−δ)τ. (3)

From Equations (2) and (3), we see that the futures price f is the expected future spot price in the risk neutral world.   金融数学代考

Suppose you are given the following information regarding light crude oil futures prices on Feb 20, 2010 in $US/barrel:

The dates refer to the expiry dates of the particular contracts.  Expiry dates are on    the closest business day  to the 20th of the month. Use this information to estimate  the risk adjusted drift rate for the price of oil between March 2010 and April 2010. Compare this to the rate implied between March 2010 and Sept 2010, as well as between March 2010 and March 2011. Assuming a risk free rate of 1%, what are the implied convenience yields?

更多代写：北美留学生代写  Gmat代考  北美商科代修网课  北美网课代写修改润色  北美论文assignment代写  为什要选择网课代修

合作平台：essay代写 论文代写 写手招聘 英国留学生代写