ECON2070
PRACTICE ON EXTENSIVE FORM GAMES WITH PERFECT
INFORMATION
金融学经济学代写 If Player 2 agrees, both players get a payoffff of 0, regardless of the actual colour of the card and the announcement.
This is an optional exercise for you to get some practice on Extensive Form Games with Imperfect Information. There is no need to turn this in.
Question 1
(Level A) Consider the following simple poker game. Nature fifirst draws either a red card or a black card with equal probabilities and reveals it to Player 1. Player 1 then announces either red or black. (Her announcement need not be truthful.)Player 2 does not see the colour of the card drawn but hears Player 1 announcement.Upon hearing an announcement, Player 2 can choose to agree or disagree. If Player 2 agrees, both players get a payoffff of 0, regardless of the actual colour of the card and the announcement. If Player 2 disagrees, the card is revealed. If the colour of the card is the same as Player 1’s announcement, Player 1 gets a payoffff of 1 while Player 2 gets −1. If instead the colour of the card is difffferent from Player 1’s announcement, Player 1 gets−1 and Player 2 gets 1.
(a) Represent this game by drawing a game tree. (You do not need to solve the game.)
(b) List all pure strategies of Player 1 in this game.

Question 2 金融学经济学代写
Consider the following Battle of the Sexes with the option of staying home(this is from Lecture 12):
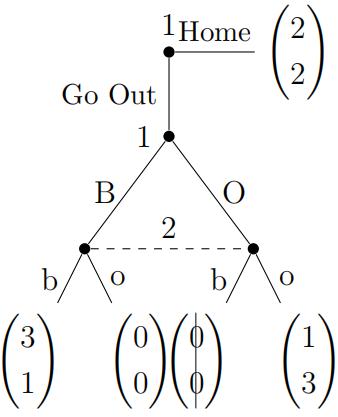
(a) (Level A) Identify all subgames in this game tree.
Date: May 10, 2021.
1(b) (Level B) Solve for all subgame perfect equilibria of this game. (Hint: there are three.)
Question 3 金融学经济学代写
An incumbent fifirm (Player 1) has been the monopolist in the market of widgets but things may be changing now. There is a small company (Player 2) researching on a new production technology of widgets. The incumbent does not know if the research is successful, but estimates that the research will fail with probability p, where 0 < p < 1.
The incumbent has to decide, before knowing the outcome of the research, whether it should acquire (A) the small company (and integrate the technology) or launch a big advertisement campaign to deter (D) the small company from entering the market. If the incumbent acquires, the small fifirm always accepts and the game ends. If the incumbent deters, the small fifirm can choose to stay out (O/o) or enter (E/e) the market. The game tree is given as follows (the fifirst payoffff is the incumbent’s and the second payoffff is the small company’s):
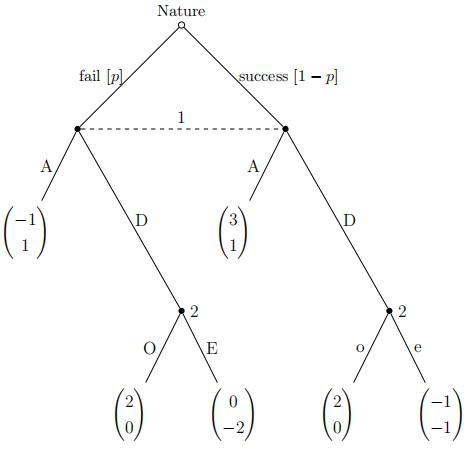
(a) (Level A) Identify all subgames in this tree.
(b) (Level B) What would player 2 do at each of his decision nodes in a subgame perfect equilibrium?
(c) (Level B) For what values of p would player 1 choose A in a subgame perfect equi librium?

