HPC in Finance代写 Assignments代写 C++ 代写 Python代写

FINM 32950: Intro to HPC in Finance

HPC in Finance代写 Complete the following assignments before the deadlines:You may collaborate, use the Internet and books.

Assignments 1-7

June 28, 2019

Common Items

Assignment 1: Due: July 5 by 6 PM (CST)

Assignment 2: Due: July 5 by 6 PM (CST)

Assignment 3: Due: July 12 by 6 PM (CST)

Assignment 4: Due: July 12 by 6 PM (CST)

Assignment 5: Due: July 12 by 6 PM (CST)

Assignment 6: Due: July 19 by 6 PM (CST)

Assignment 7: Due: July 19 by 6 PM (CST)

Instructions HPC in Finance代写

Complete the following assignments before the deadlines:

•  You may collaborate, use the Internet and books.
•  Be sure to list the names of collaborators, urls and books used.

The aims of the initial assignments:

1.Get everyone up to speed with

2.Theseproblems will be used to introduce new concepts and techniques.

Common Requirements HPC in Finance代写

• Use the specified programming language.
• Do not just submit work you did for Computing for Finance in C++ course assignments:
• Pay attention to performance
• No need to focus on reusability and extensibility
• Write the fastest program you can write using C++ (or Python) you already know well.
• You don’t have to spend time to learn new topics (e.g. multithreading) on your own to do these assignments.
• Performance at any level is acceptable.
• Performance at any cost is also acceptable.
• You may do these assignments on Windows or Linux or Mac.

Grading

Each counts (equal weight) towards the final grade.

To get full points:

make a genuine and honest effort to solve a problem

it is ok if the solution is not complete/correct/ideal HPC in Finance代写

should submit before the deadline

Common Notations

We use the following notation:

S_t : Stock price at time t

σ : Volatility of the Stock (assumed constant)

r : Interest rate

T : Time to option expiration (in years) K : Strike price

W_t : Brownian motion process N(0, 1) : Standard normal distribution (A − B)+ : Max(A-B, 0)

Useful Items HPC in Finance代写

Generating Random Inputs

Where applicable, you may use the function shown below to generate input values randomly:

float random_data(float low, float hi)

{

float r = (float)rand() / (float)RAND_MAX; return low + r * (hi - low);

}

Measuring Running Time using Chrono

• We use a timer to measure how much it took to run a piece of code.
• Generally, we would call an operation a sufficient number of times and get the average execution time.HPC in Finance代写
• We have many choices to get timing measurements. Code snipper below shows how to use chrono in the C++ Standard Library.

using namespace std::chrono; high_resolution_clock::time_point t1 =

high_resolution_clock::now();

do_something(); high_resolution_clock::time_point t2 =

high_resolution_clock::now();

std::cout << "Elapsed time: " << duration_cast<milliseconds>(t2 - t1).count() << " ms";

• Defined in chrono header.

Assignment 1 (C/C++) HPC in Finance代写

Due: July 5 by 6 PM.

• Write a function to multiply two NxN matrices.
• Use the function you wrote to multiply two 100×100 matrices.
• Measure execution time.
• Vectorizing/parallelizing code is NOT required.
• There are many ways to represent a matrix. Any method, including the following, is acceptable.

use a library: e.g. Eigen

use std::vector:

using  matrix   =   std::vector<std::vector<float>>; or

typedef std::vector<std::vector<float>> matrix;

...

Assignment 2 (C/C++)

• Due: July 5 by 6 PM.
• Write a function to price European Call options using Black Scholes formula.
• Use it to price 1 million options.
• Measure time taken to price 1 million options.
• Vectorizing/parallelizing code is NOT required.HPC in Finance代写

Assignment 3(C/C++)

Due: July 12 by 6 PM.

• Write a function to price European style Call options using a binomial tree.
• Jarrow-Rudd tree is explained below but you may use any other type (e.g. CRR) of your choice.
• Measure time taken to price 1 million options.
• Vectorizing/parallelizing code is NOT required.

The Jarrow-Rudd Binomial Tree

• We will use a binomial tree to simulate the paths of the underlying stochastic process.
• Jarrow-Rudd tree assumes the random value (z=N(0, 1)) takes +1 or -1 with equal (risk neutral) probability of 1/2 at every node in the tree.
• If we know the stock price at time t, Equations 1 and 2 give us possible values for the stock prices at time t + ∆t.

Stock Price Process

This leads to stock price at time t + ∆t:

z = 1 : SU = St exp((r −σ²/2)∆t+σ√∆t) (1)

z = −1 : SD = St exp((r −σ²/2)∆t−σ√∆t) (2)

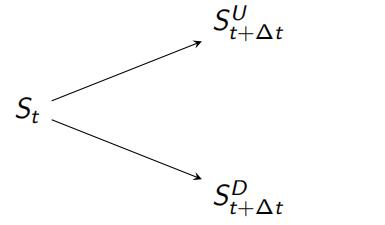
• We refer to these two stock prices as SUt+∆t and StD +∆t to mean the stock prices at up and down nodes respectively, at time t + ∆t.

• We simulate how the stock prices would evolve on the tree using Equations 1 and 2:
• divide time to expiration, T , into equal N parts such that∆t = T /N
• discretize W_t such that

∆W_t = √∆tN(0, 1)   (3)

and assume the underlying Brownian motion can only move a fixed amount up or down at each time step.HPC in Finance代写

(In the case of Jarrow-Rudd tree, the random variable N(0, 1) given in Equation 3 takes +1 or -1 with an equal probability of 1/2.)

we start from the left of the tree, i.e. t = 0 and build the binary tree for the stock price process at every ∆t increment

A full binomial tree with 3 times steps (N=3) is shown next.

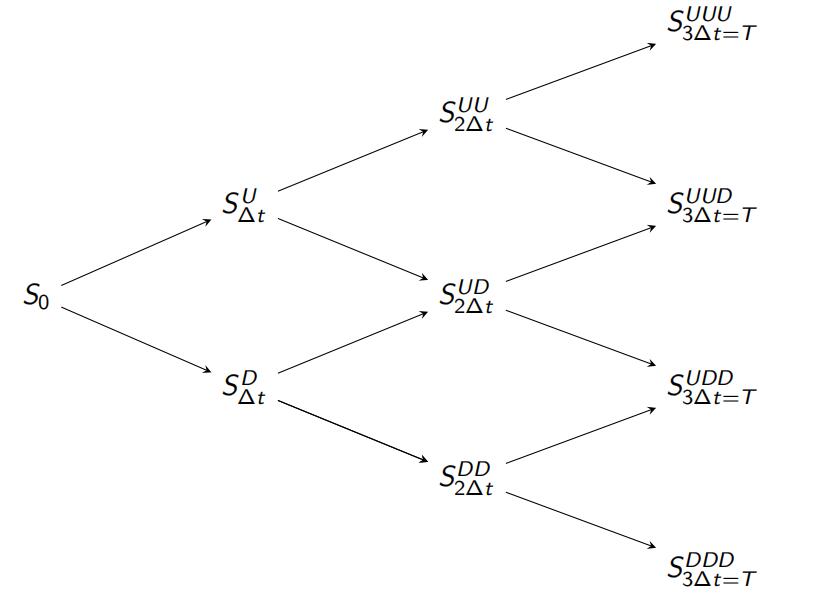
Such a construction yields a binomial tree.

This tree recombines by construction.

Recombining means: if you start from a node at time t, an up move at time t followed by a down move at time t + ∆t and a down move at time t followed by an up move at time

t + ∆t end up at the same node at time t + 2∆t

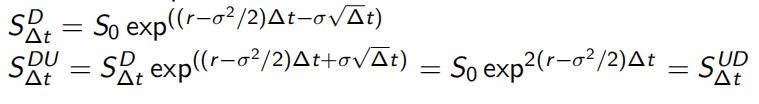
Recombining trees do not grow very large when we increase the number of time steps.

Note:

1.The arrows show the direction of pathsimulation.

2.SuperscriptsD, DD, U, UU  denote how many levels the stock price has gone up or down from the initial value.

U denotes an up movement; D denotes a down movement.

Pricing an European Option

We use the stock prices at each node on the tree to calculate the option price:

e The option payoff at time t=T, i.e. C (S_T ), is given by the options payoff function.

Call: C (S_T ) = max (S_T − K , 0)

Put: C (S_T ) = max (K − S_T , 0)HPC in Finance代写

e The option payoff at time t, C (S_t), is given by the discounted expectation of the option payoffs at time t + ∆t: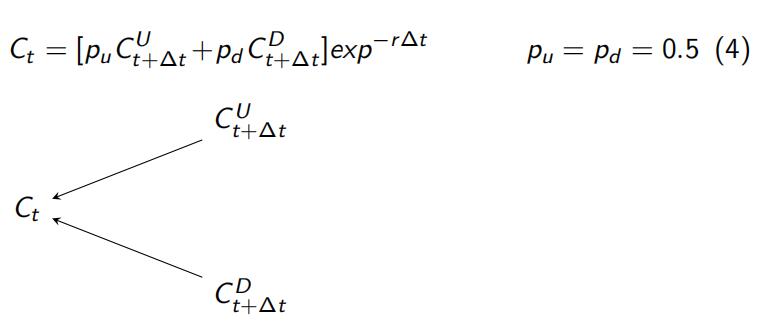

 

 

 

 

 

Pricing an European Option

Risk neutral probabilities associated with each path (p_u and

p_d ) is 0.5 (by construction) for Jarrow-Rudd trees.

Starting from the right (t = T ) back-propagate the option prices to find the price of the option at time zero.

The price of option at time t, i.e. C_t is given by the discounted expectation of prices at time t + ∆t, given in Equation 4.

Notes: HPC in Finance代写

1.The arrows show the direction of the

2.SuperscriptsD, DD, U, UU  correspond to the stock price levels.

3.0.5Risk neutral probability value in Equation 4 applies to Jarrow-Rudd trees only. Other types of trees may have different risk neutral probabilities.

A full binomial tree with 3 time steps (N=3) is shown below:

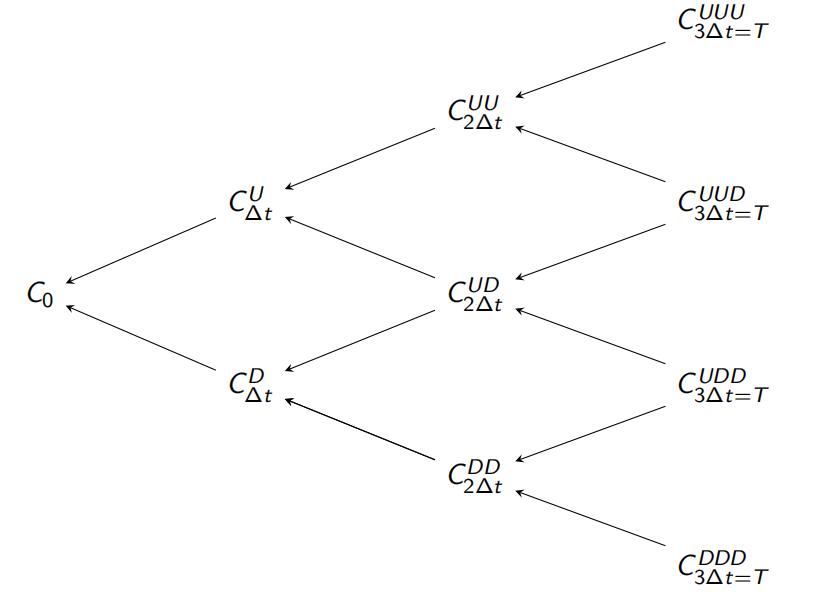
The option price at time zero (t = 0) is given by C₀.

Assignment 4 (C/C++)

Due: July 12 by 6 PM.

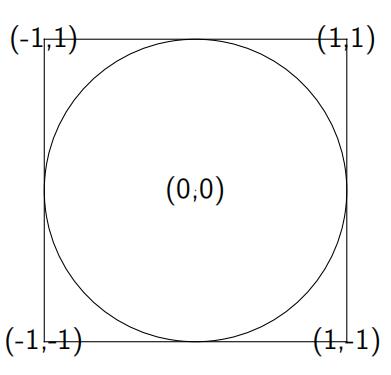
A simple Monte Carlo simulation can be used to approximate the value of π.

The figure below shows a circle with radius r = 1 inscribed within a square.

The area of the circle is πr 2 = π, and the area of the square is (2r )2 = 4. The ratio of the area of the circle to the area of the square, ρ, is given by:

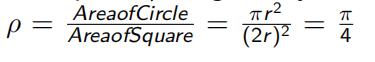
Calculating the value of π using Monte Carlo involves the following steps:

1.Assumethe circle is centered at coordinates (0, 0).

2.GenerateN random points with coordinates (x, y) where x and y are independently drawn from a uniform distribution over the interval [-1, 1].

3.Determineif each point lies inside the circle or not

The value of π can be estimated using the simulation results as follows.

where, N = total number of points generated and M = number of random points inside the circle.HPC in Finance代写

Write a program to calculate the value of π using information above, for N = 100, 1000 and 10000. Write the results to the standard output.

Vectorizing/parallelizing code is NOT required.

Assignment 5 (C/C++) HPC in Finance代写

Due: July 12 by 6 PM.

Write a function to price European Call options using Monte Carlo.

Use the function you wrote to price 1 million options.

You may use the function shown below to generate input values randomly:

Measure time taken to price 1 million options.

Vectorizing/parallelizing code is NOT required.

Monte Carlo Technique: Background

The (time 0) value of an option is the discounted expectation

of its payoff under the risk neutral measure1.

That means: to price an option we need to compute an

expected value, i.e. an integral.HPC in Finance代写

Monte Carlo is a numerical technique used to estimate an integral.

1http://en.wikipedia.org/wiki/Risk-neutral_measure

Stock Price SDE

We assume a stock price process follows a Geometric Brownian Motion2.

Under the risk neutral measure the process of the stock price is given by the SDE:

dS_t = rS_tdt + σS_tdW_t (5)

where,

dW_t = N(0, dt) (6)

W_t  = √tN(0, 1) ∵ W₀ = 0 (7)

I.e. The Brownian motion has a normal distribution with mean zero (0) and variance t.

Using the above SDE we get:

St  = S0 exp((r −σ²/2)t+σ√tN(0,1)) (8)HPC in Finance代写

2http://en.wikipedia.org/wiki/Geometric_Brownian_motion

Using equation (4), we can simulate the stock price at any time t, in the future.

N(0, 1) is a random observation (random number) drawn from the standard normal distribution.

Let’s say, z = a random number drawn from N(0, 1).

The stock price at the expiration (time T) is given by:

ST  = S0 exp((r −σ²/2)T +σz√T (9)

That means, we can simulate the terminal stock price S_T (i.e. price at time T ).

What do we need to find the price of a European style option?

Monte Carlo Option Pricer: Step by Step

Draw a random number (z_i ) from the standard normal distribution, N(0, 1). Here, the subscript i denotes the ith draw.HPC in Finance代写

Simulate the stock price at the option expiration (S_T ). The stock price at the expiration is given by:

ST ,i = S0 exp((r −σ²/2)T +σz_i √T (10)

e For a given price path (ithrealization), the European call payoff at time zero is given by:

C_i = exp−rT (S_T ,i − K )+ (11)

Repeat above steps for (M) trials, and calculate the option payoff for each path.

Find the mean value of the option payoffs:

Cˆ = exp−rT  ΣM  (S K )+ (12)

Monte Carlo Option Pricer: Step by Step

This is an estimate of the option price.HPC in Finance代写

The law of large numbers states that such an estimate converges to the correct value as the number of trials (M) increases.

Assignment 6 (Python)

Due: July 19 by 6 PM.

Write a function to price European Call options using Black Scholes formula.

Use it to price 1 million options.

Measure time taken to price 1 million options.HPC in Finance代写

Assignment 7 (Python)

Due: July 19 by 6 PM (CST).

Write a program to generate a normal Julia set.

Plotting is not required.

Measure time taken to run the program.HPC in Finance代写

Info about Julia sets can be found at:

https://en.wikipedia.org/wiki/Julia_set

更多其他：C++代写 java代写 r代写 代码代写 金融代写  python代写 web代写 物理代写 数学代写 考试助攻 计算机代写 C语言代写

合作平台：天才代写 幽灵代写 写手招聘 Essay代写