Operations Research
exam
Duration: 2h30
运筹学考试代写 1.The following Linear Programming model refers to the production planning of a monthly dose of a food supplement.
Notes:
- Justify your answers.
- Do not detach the sheets.
- Do not use neither pencil nor red pen to write your answers.
- No electronic devices are allowed.
- The marks are given at the end of each question.
1. 运筹学考试代写
The following Linear Programming model refers to the production planning of a monthly dose of a food supplement.
The decision variables represent the amount, in kilograms, of three constituents (C1, C2, and C3) to be added to the monthly dose of the food supplement. These constituents contain some nutrients, namely N1, N2, and N3. The first three constraints state the minimum amount, measured in units, of nutrients N1, N2 and N3 required on each monthly dose of the food supplement, whereas the fourth constraint is related with the maximum amount of constituent C2, given in kilograms, that is available. The objective is to minimize the acquisition cost of the constituents.
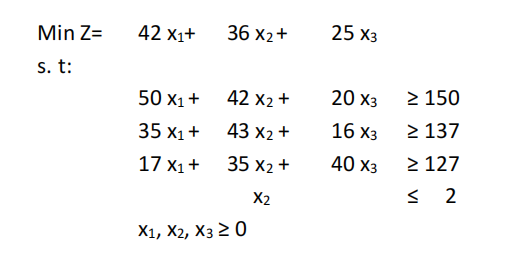
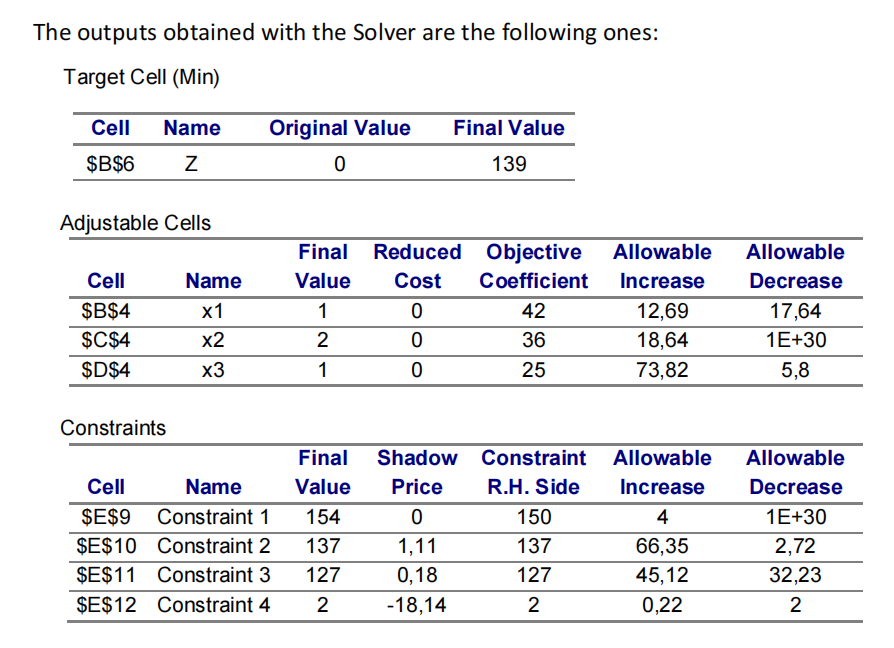
a) Indicate the optimal composition of the monthly dose of the food supplement,the optimal total acquisition cost, and analyse each constraint on the context of the Justify. [1.5]
b) Suppose the per kg acquisition cost of the constituent C1 has to be increased by 5 c.u. What would be the consequences on the optimal plan and on the total acquisition cost? Justify. [1.0]
c) Due to new policies established by the Health Mundial Organization, the supplement must contain at least 137 units of nutrient N3. What would be the consequences of this new requirement? Justify. [1.25]
d) Suppose that it is possible to acquire more 100 grams of constituent C2. However, the per kg acquisition cost of these additional units is 44,14 c.u. instead of 36 u.m, as it was. Would this acquisition be advantageous? Justify. [1.5]
2. 运筹学考试代写
An enterprise manufactures three products, P1, P2, and P3. Three raw materials MP1, MP2, and MP3 are used to make the aforementioned products. The units of raw materials required per kg of product are given in the next table:
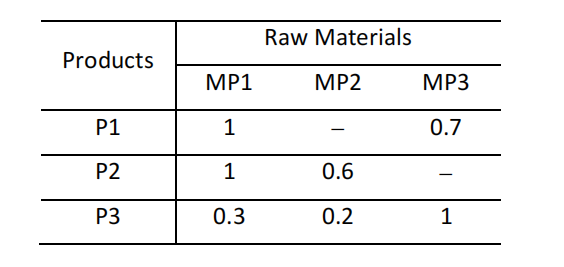
The enterprise estimates that the sales of products P1, P2, and P3 will not exceed 1000, 1500, and 2000kg, respectively. By the other side, the commitments with suppliers guarantee up to 2000, 1500, and 2000 units of raw materials MP1, MP2, and MP3, respectively.
In the table below, the sales price of each kg of product as well as the unit acquisition cost of raw materials are given.
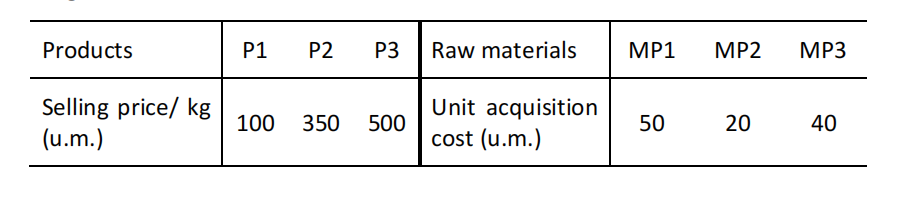
a) Having as objective to maximize the total profit, formulate as a LinearProgramming problem in order to determine the amount of each product that should to be produced. Do not forget to mention the meaning of the decision variables and to give a brief explanation about the meaning of the constraints.[1.75]
b) Suppose now that products P2 and P3 require the other products to be More precisely, each kilogram of P2 requires 2 kilograms of P1, whereas 1.2 kilograms of P2 are needed to produce one kilogram of P3. Whichchanges should be made in the formulation presented in a) in order to accomplish this new requirement? [1.5]
c) Suppose now that the unit profit of P3 depends on the sales’ level, namely if more than 1200 kilograms are sold, then the per kg selling price will be 400 c.u., otherwise it will be 460 c.u.. Which changes should be made in the formulation presented in a) in order to accomplish this new requirement?[1.25]
3. 运筹学考试代写
The packaging section of a given factory houses two machines, M1 and M2, whose monthly capacity is 160 and 140 hours, respectively. On this section, 400 and 200 units of products P1 and P2, respectively, are monthly packaged. The time required to pack one unit of P1 and P2 is 15 and 30 minutes, respectively for P1 and P2, regardless of the machine used. The packing cost, in c.u. of each unit of product on each machine is given in the following table:
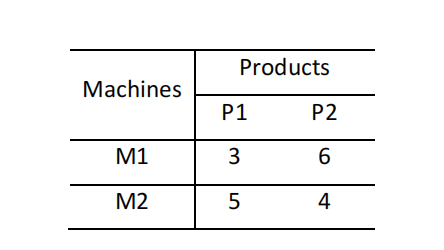
Knowing that products should be packed so as to minimize the cost, draw a network representing the problem. Identify the network problem that would allow determining the optimal packing plan. Justify. [1.5]
4. 运筹学考试代写
Consider the following network, where the nodes represent checkpoints and the values next to edges indicate the minimum distance, in meters, between the checkpoints:
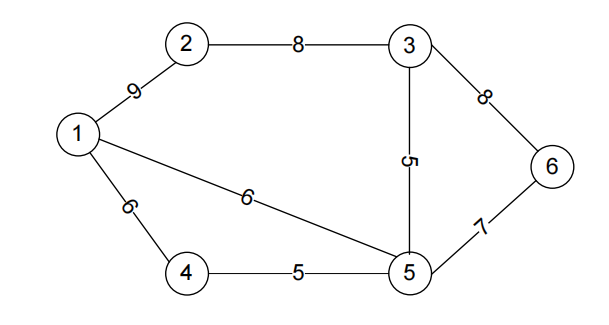
Being the objective to establish a communication network between the different checkpoints so as to minimize the installation cost, and knowing that the installation cost is proportional to the distance, which links should be chosen? Justify using the problems of network models. [1.5]
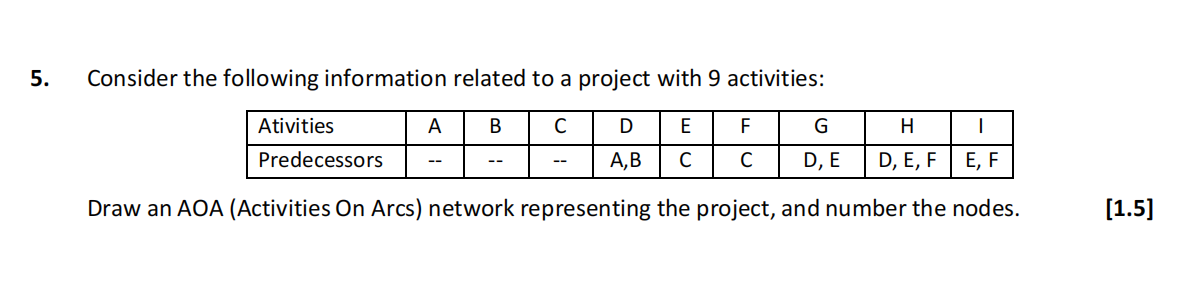
6.
Consider the following AON network representing a project with 6 activities, and whose durations are measured in weeks:
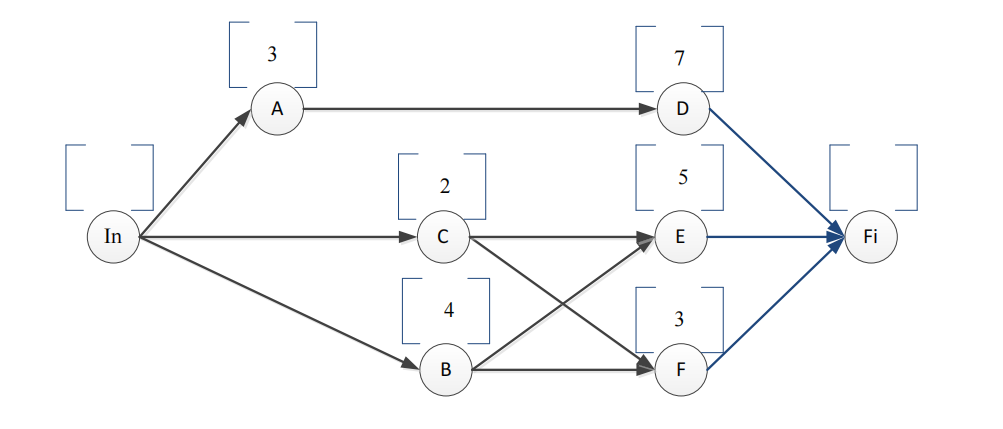
a) Determine the minimum project duration. Justify.[1.25]
b) Determine the critical activities and the critical path(s). Justify. [1.75]
Consider the following information:
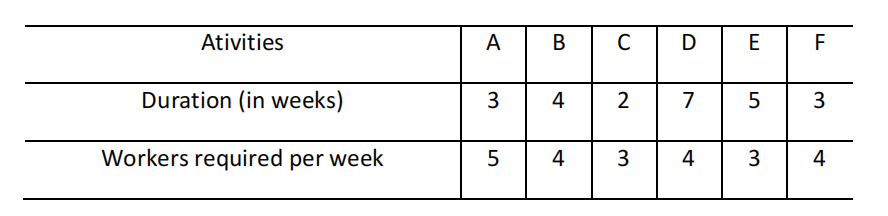
c) Suppose the project manager has 10 workers available per week to be assigned tothe project, and that he wants to determine a predecessor-feasible andresource-feasible schedule. Knowing that priority is given to activities that last for more time, apply the SGS-parallel heuristic to find it. Do not forget to indicate the schedule and to give the project duration. [1.75]
7. 运筹学考试代写
Consider the following AON network representing a project:
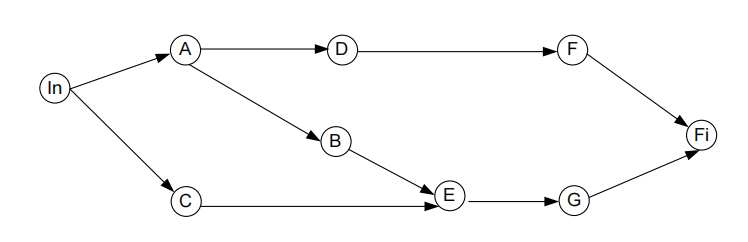
The minimum project duration is 8 days and the critical activities are A, B, C, E, and G. What would be the consequences on the project duration, critical activities and critical path, if the duration of activity B is decreased by 1 day? Justify. [1.0]

更多代写:国外留学生计算机代上网课价格 雅思代考 英国金融online quiz代考 建筑设计Essay代写 教育学毕业论文代写 留学网课代修代上
