OPERATIONS RESEARCH
Exercises
Network Models
运筹学网络模型代写 Ex 3 Six farmers decided to get together and build the water system for their farms. The water system consists of one well (point A),
Ex 3
Six farmers decided to get together and build the water system for their farms. The water system consists of one well (point A), several water tanks, which will be installed on each farm, and the canal system to provide water to all tanks. The distance between the well and the water tanks as well as between the water tanks are as follows (in meters):
| Point A | Tank 1 | Tank 2 | Tank 3 | Tank 4 | Tank 5 | Tank 6 | |
| Point A | 0 | 100 | 150 | 20 | 80 | 100 | 50 |
| Tank 1 | 0 | 80 | – | 100 | – | – | |
| Tank 2 | 0 | 20 | – | – | – | ||
| Tank 3 | 0 | – | – | 10 | |||
| Tank 4 | – | 30 | – | ||||
| Tank 5 | 0 | 150 |
The distances marked with “-” are related to connections which are technically impossible. The cost of this water system is proportional to the extension of the canal network. Given that the farmers want the most economical water system, draw a network representing the problem. Solve the problem and describe the obtained solution, indicating the optimal extension of the canal system.
Ex 6 运筹学网络模型代写
Company Alfa-Tools wants to choose some equipment to produce a certain product for the next 4 years. Each equipment has a lifetime duration. For example, equipment of type A must be replaced every year, type B every two years and type C every three years. It is expected that equipment cost (at constant prices) decrease in value as time goes by. The available information is the following:

Knowing that the company intends to determine the most economical plan for the acquisition of the equipment to be used in the next four years:
a) Draw a network representing the Alfa-Tools situation and identify the network problem.
b) Solve the problem and interpret the optimal solution and the optimal value.
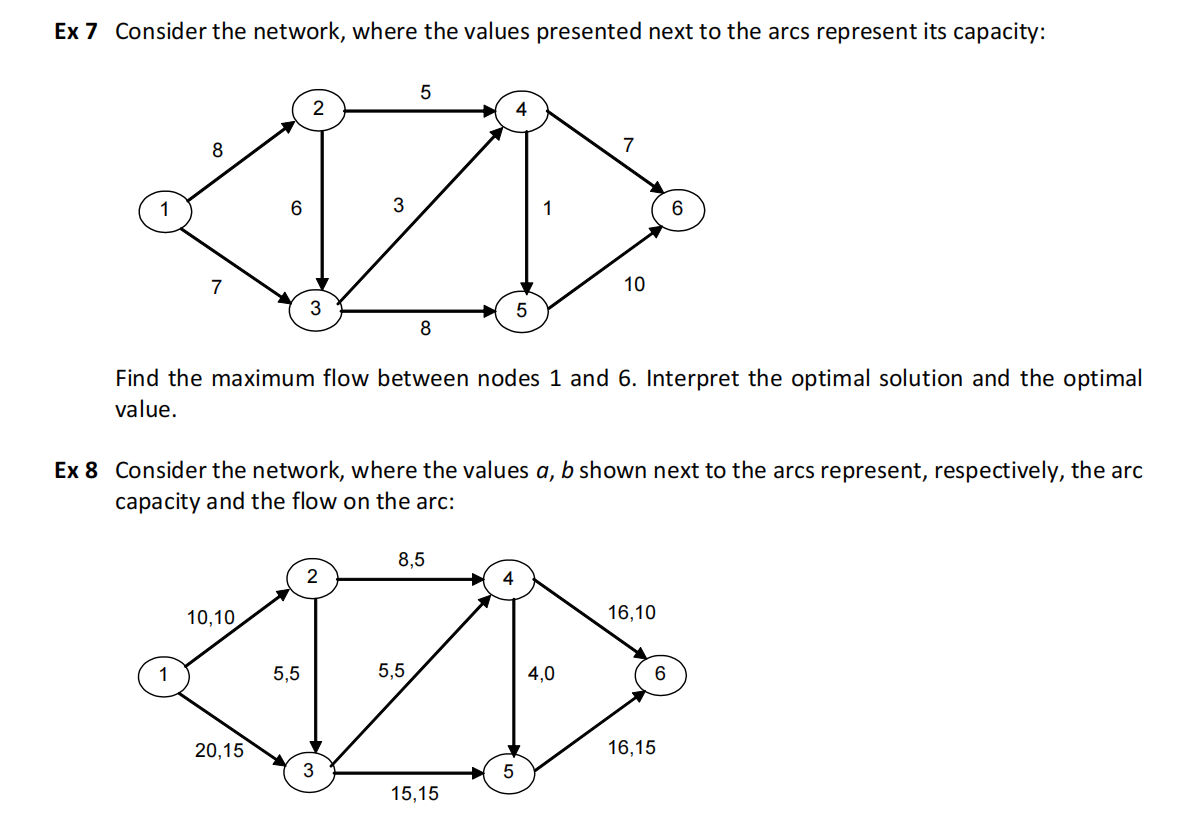
a) Determine the flow value on the network and identify the saturated arcs.
b) Find the maximum flow between nodes 1 and 6. Interpret the optimal solution and the optimal value.
Ex 9 运筹学网络模型代写
The network represented below relates to a water system. Each arc represents a conduct and the vertices represent the connecting points between conducts. The value next to each arc represents its capacity (in thousands of liters), per minute.
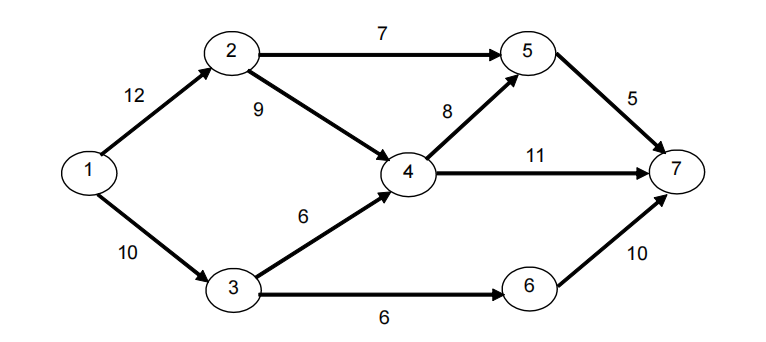
The objective is to determine the maximum quantity of water that can flow, per minute, from point 1 to point 7.
a) Identify the network problem that represents this situation.
b) Find the optimal solution and interpret it, as well as the optimal value.
Ex 10 Consider the networks:
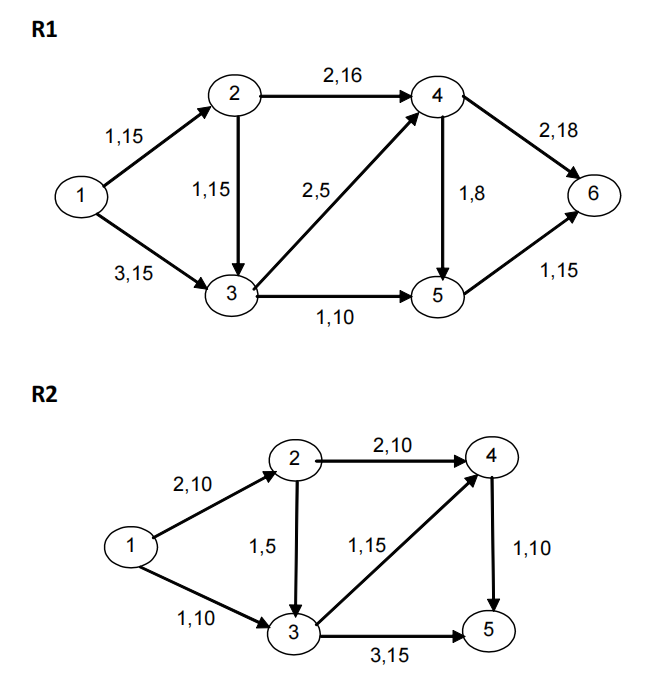
where the values a, b shown next to the arcs represent, respectively, the arc capacity and the flow on the arc.
a) In R1, find the minimum cost flow with value 24 between nodes 1 and 6. Interpret the optimal solution and the optimal value.
b) In R2, find the minimum cost flow with value 17 between nodes 1 and 5. Interpret the optimal solution and the optimal value.
Ex 11
A company must transport 25 tons of a certain product from point A to point F. Direct transportation from A to F is not allowed. Thus, intermediate points have to be used. The unit transportation costs and the transportation capacities associated to each link are indicated, by this order, next to the arcs.
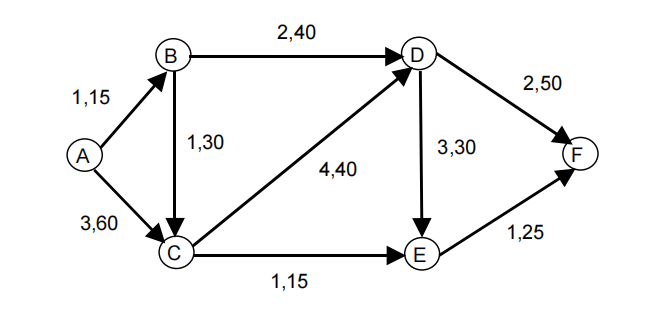
Identify the network problem that allows finding the minimum transportation cost plan and solve it. Interpret the optimal solution and the optimal value.
Ex 12
A traineeship program for young graduates may be completed in different ways. In the following network each arc represents each stage. Each traineeship is made of a sequence of stages, making a path between s and t. The values indicated close to each arc represent, respectively, the unit cost of the stage and the number of trainees that may perform the stage.
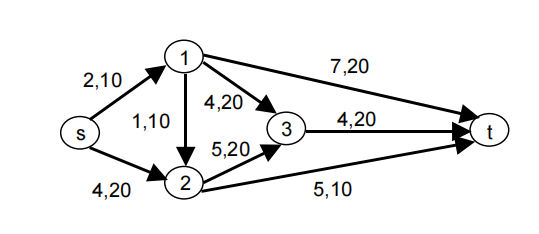
a) What is the maximum number of traineeships that can be performed? Identify the network problem and solve it. Interpret the optimal solution and the optimal value.
b) What is the most economical way to finish a traineeship? Identify the network problem and solve it. Interpret the optimal solution and the optimal value.
c) What is the most economical way of performing twenty traineeships? Identify the network problem and solve it. Interpret the optimal solution and the optimal value.
Ex 13 运筹学网络模型代写
Consider the following network representing a touristic map of a city, where node A represents a tourism post of information and the remaining nodes represent museums. Since the tourism post and the museums need to exchange information, it is necessary to install a communication network.
The values indicated close to the links represent the distance (in km) between each pair of museums and between the tourism post and each museum. The network installation cost is directly proportional to its length. It is also known that the gap time between sending the information and receiving it increases 0.001 seconds, per each kilometer covered. The objective is to install the communication network as economically as possible and to guarantee the least waiting time between sending information from the tourism post and its reception at museum F.
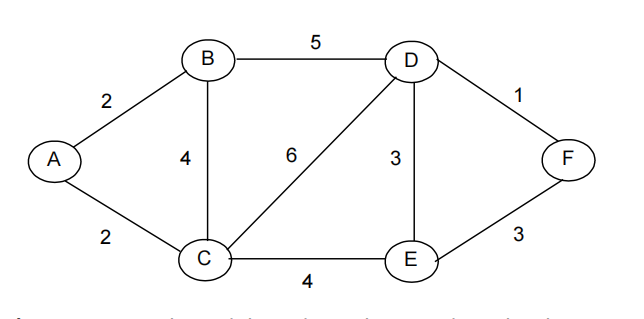
a) Using network models, indicate how to describe this situation.
b) Determine the complete optimal solution, as well as the optimal value, and interpret them.
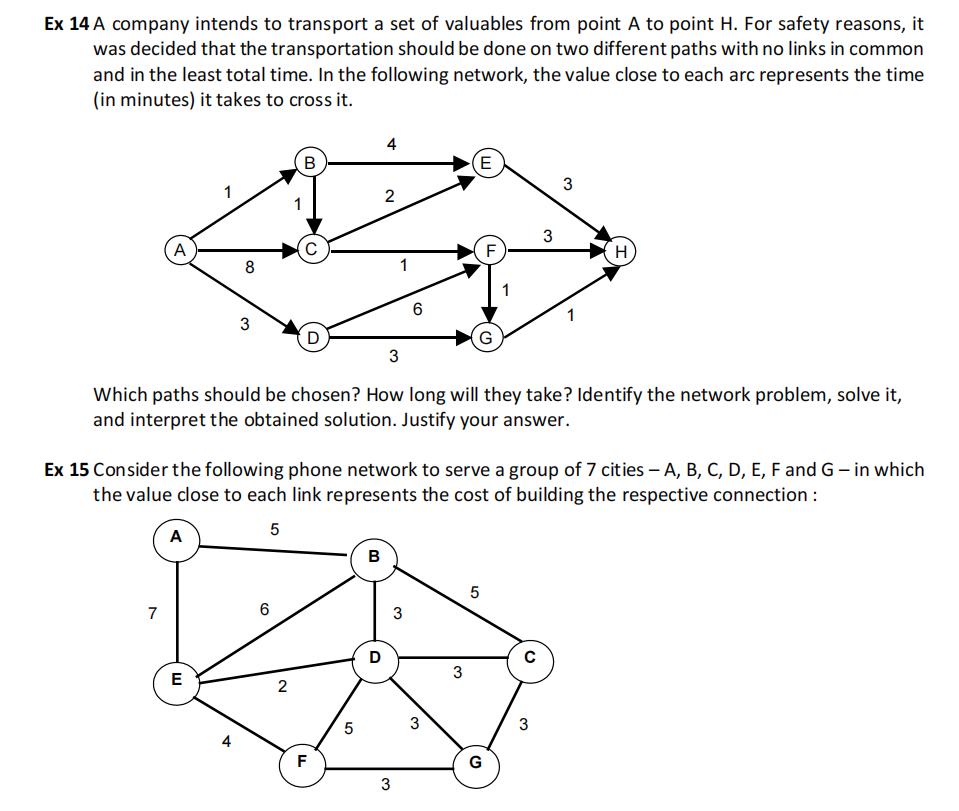
It is known that the connection (A,E) is of high priority, and so have to be chosen. In order to guarantee the phone connection between all the cities, which links should be established so as to minimize the total cost? Identify the network problem, solve it, interpret the obtained solution, and present all the justifications.
Ex 16 运筹学网络模型代写
A company must deliver seven types of parcels. It has a fleet of five trucks. There are three units of each type of parcel and the trucks’ capacities are 6, 4, 5, 4 and 3 units, respectively. Model the problem as a network problem so that no truck takes more than one unit of each type of parcel. Identify the problem.
Ex 17
An airline company is planning an extra flight from city 1 to 6. However, this flight cannot be a direct one. In the following network the cities are represented in the vertices and the arcs represent the possible flights. The value close to each arc represents the cost of the respective flight.
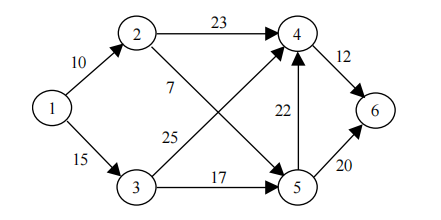
a) If the objective is to perform the most economical flight from city 1 to 6, indicate which stops should be chosen. Identify the network problem, solve it and interpret the obtained solution, as well as its value.
b) If the objective is to perform the flight from city 1 to 6 with the least number of stops, how would you solve this problem (without actually solving it)? Justify your answer.
Ex 18 运筹学网络模型代写
A company wants to plan its production for the next three months. Monthly production can be used to meet the demand for that month or to be stored and subsequently used to meet demand levels for later months. The quantities to be supplied, the production capacities and the production costs are as follows:
| Month 1 | Month 2 | Month 3 | |
| quantity to be supplied (units) | 150 | 170 | 160 |
| Production capacity (units) | 220 | 150 | 180 |
| Unit production cost (c.u.) | 10 | 12 | 15 |
There are no limitations on the amount that can be stored. The storage cost of each unit is 2 u.m. per month (storage is not considered for units produced and sold in the same month). How should production be planned in order to minimize production and storage costs? Represent this situation in a network and identify the Network Models problem associated with it.
RESUMED SOLUTIONS 运筹学网络模型代写
NOTE: Solutions must always be interpreted according to the context of the problem.
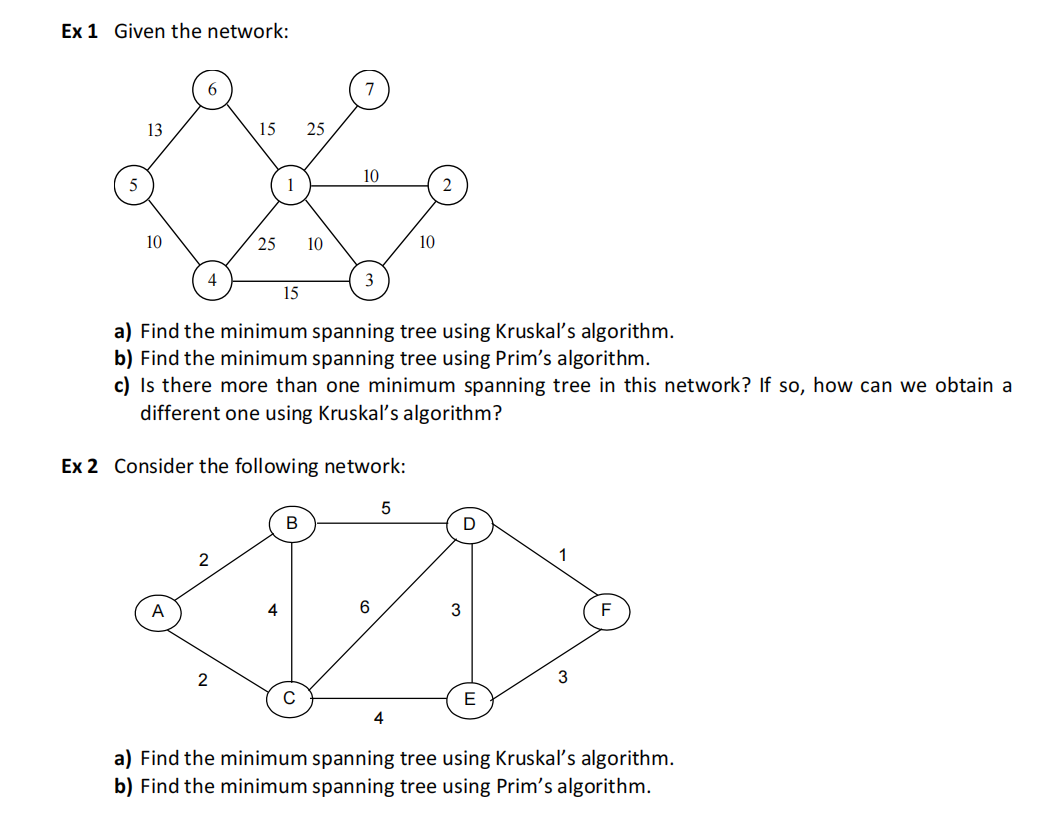
Ex 1
a) and b) several feasible solutions; TS={(1,2),(2,3),(3,4),(4,5),(5,6),(1,7)} is one of the solutions; Cost = 83
c) Consider another way of sorting {(1,2),(2,3),(1,3)}.
Ex 2
a) e b) two feasible solutions; TS={(A,B),(A,C),(C,E),(D,E),(D,F)} is one of them; Cost = 12
Ex 3
TS = {(T1,T2), (T2,T3), (A,T3), (A,T4), (T4,T5), (T3,T6)}; extension = 240 m.
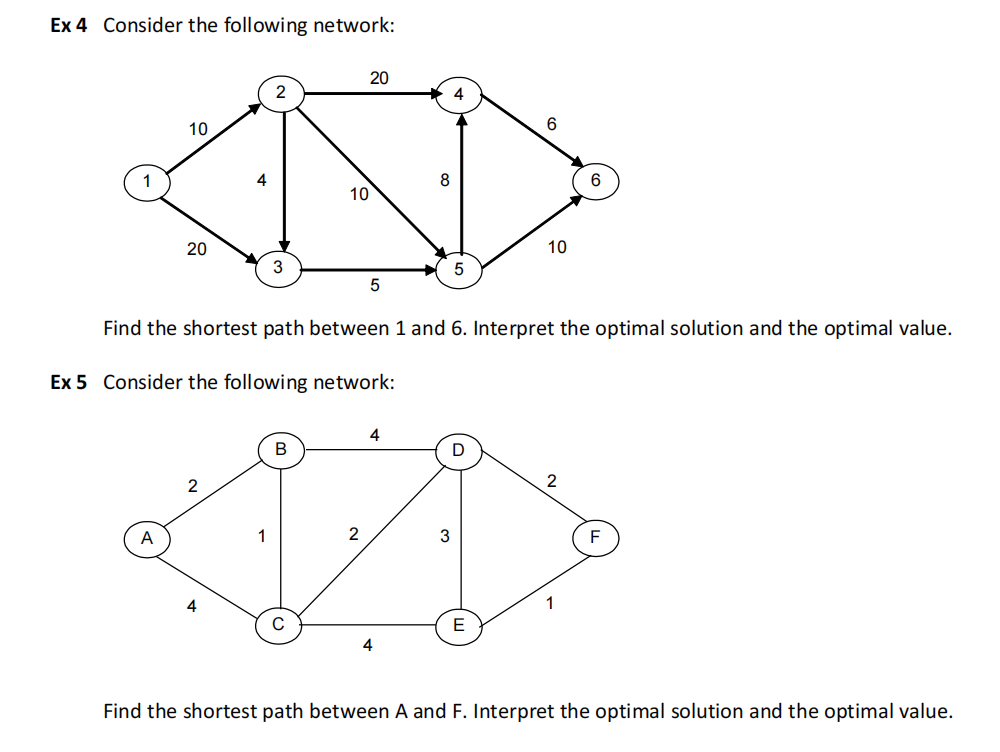
Ex 4
Linear Programming Model in Excel file.
The shortest path between 1 and 6 is {(1,2),(2,3),(3,5),(5,6)} with length equal to 29 (see Answer Report of Solver).
Ex 5 运筹学网络模型代写
Linear Programming Model in Excel file.
The path is {(A,B), (B,C), (C, D), (D,F)}, with length equal to 7 (see Answer Report of Solver).
Ex 6
b) Linear Programming Model in Excel file. The equipment C is chosen for the first three years and equipment A is bought for the forth year. The total cost is equal to 270 (see Answer Report of Solver).
Ex 7
Linear Programming Model in Excel file.
Optimal Solution: x12=x35=x56=8, x13=x46=7, x24=5, x23=3, x34=2, x45=0.
Maximum Flow Value = 15 (see Answer Report of Solver).
Ex 8
a) Flow Value = 25. Saturated Arcs: (1,2), (2,3), (3,4), (3,5) .
b) Linear Programming Model in Excel file.
Optimal Solution: x12=x24=8, x13=20, x23=x45=0, x34=5, x35=x56=15, x46=13.
Maximum Flow Value = 28 (see Answer Report of Solver).
Ex 9 运筹学网络模型代写
a) Maximum Flow between 1 and 7.
b) Linear Programming Model in Excel file.
Optimal Solution: x12=12, x13=10, x24=7, x25=x57=5, x34=4, x36=x67=6, x45=0, x47=11.
From point 1 to point 7, it is possible to pass 22 thousand of liters, per minute (see Answer Report of Solver).
Ex 10 a) Linear Programming Model in Excel file. Cost = 119, x12 = 15, x13 = 9, x23 = 1, x24 = 14, x35=10, x46 = 14, x56 = 10, on the other arcs the flow is null (see Answer Report of Solver).
b) Linear Programming Model in Excel file. Cost = 72, x12= 7, x13= 10, x24 = 7, x34 = 3, x35 = 7, x45 = 10, on the other arcs the flow is null (see Answer Report of Solver).
Ex 11 Minimum Cost Flow from A to F with value q=25.
Cost = 120, xAB = 15, xAC = 10, xBC = 5, xBD = 10, xCE = 15, xDF = 10, xEF = 15, on the other arcs the flow is null (see Answer Report of Solver).
Ex 12 运筹学网络模型代写
a) Maximum Flow between s and t. Linear Programming Model in Excel file.
Optimal Solution: xs1=x13=x23=x2t=10, xs2=x3t=20, x12=x1t=0.
Maximum Flow Value = 30 (Maximum number of traineeships): see Answer Report of Solver.
b) Shortest Path between s and t. Linear Programming Model in Excel file. Traineeship: (s,1), (1,2), (2,t). Cost = 8 (see Answer Report of Solver).
c) Minimum Cost Flow from s to t with value q=20. Linear Programming Model in Excel file. Perform 10 traineeships (s,1), (1,t) and 10 traineeships (s,2), (2,t). Total Cost = 180 (see Answer Report of Solver).
Ex 13 a) Minimum Spanning Tree that includes the Shortest Path between A and F.
b) Minimum Spanning Tree that includes the Shortest Path between A and F.
Links: (A,B), (A,C), (B,D), (D,F), (D,E). Extension: 13 Kms.
Alternative Solution: (A,B), (A,C), (B,D), (D,F), (E,F).
Ex 14 运筹学网络模型代写
Minimum Cost Flow from A to H with value q=2.
The time is considered as the unit cost flow and the capacities are equal to 1.
Paths: A -> B -> C -> F -> H with duration of 6 minutes and A -> D -> G -> H with duration of 7 minutes. Total duration = 13 minutes.
(see Answer Report of Solver)
Ex 15 Minimum Spanning Tree that includes the link (A,E).
Application of Kruskal’s algorithm or Prim’s algorithm.
Links: (A,E), (E,D), (C,D), (C,G), (F,G), (B,D). Total Cost = 21.
There are other optimal solutions.
Ex 16 运筹学网络模型代写
nodes 1,..,7 – parcels; nodes C1,..,C5 – trucks; source node s; sink node t;
arcs (s,i), i = 1,…,7, with capacity = 3; arcs (i,Cj), i = 1,…,7, j = 1,…,5, with capacity = 1;
arcs (Cj,t), j = 1,…,5, with capacity equal to the capacity of truck Cj. The objective is to find the maximum flow between s and t.
Ex 17 a) Shortest Path between 1 and 6. Optimal path: 1 -> 2 -> 5 -> 6. Cost of the flight = 37. The flight stops at 2 and 5 (see Answer Report of Solver).
b) Path between 1 and 6 with the smallest number of arcs. Consider the weight of all arcs equal to 1. The problem is solved by finding the shortest path between 1 and 6.
Ex 18 Minimum cost flow problem with value equal to the total demand.

