ECMT5001: Final Examination (2021s2)
计量经济学final代做 Mimi claims that more rainfall increases the sales of umbrella. Test Mimiís claim at the 5% significance level. Show all your steps.
The total score of this exam is 60 marks. Attempt all questions. Correct all numerical answers to 2 decimal places.
1.[Total: 18 marks] Mimi owns a store which sells umbrellas. To understand about the cyclical nature of his business, he runs a linear regression of sales on rainfall, using 36 monthly observations over January 2018 – December 2020. The regression model is given by 计量经济学final代做
S = β0+ β1R + u;
where S is the monthly sales (in $1,000) and R is the monthly average rainfall in mm.
The estimated model is given by (standard errors in parenthesis):
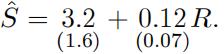 (1)
(1)
(a) [2 marks] What is the predicted monthly sales when the monthly rainfall is averaged at 100 mm?
(b) [5 marks] Mimi claims that more rainfall increases the sales of umbrella. Test Mimiís claim at the 5% significance level. Show all your steps.
(c) Baobao, Mimiís assistant, suggests to include seasonal e§ects by considering the fol-lowing regression model:
![]() (2)
(2)
where Qi is the time dummy for quarter i (i = 1; 2; 3; 4). Baobao attempted to run the regression on Stata, but an error was produced.
i.[3 marks] Explain why Stata produced an error. Which least-squares assumption
does regression (2) violate? 计量经济学final代做
ii.[2 marks] How can Baobao modify regression (2) so that it becomes a valid regression?
(d) [6 marks] Simon recommends Mimi to run the following regression
S = α0 + α1R + α2P + w;
where P is the average unit price of umbrella in a given month.
From past business records, Mimi tends to set a higher price on rainy days, and a lower price on sunny days. It is also clear that umbrella is a normal good (such that higher price is associated with lower sales, and vice versa).
Do you think the OLS estimator of β1 in regression (1) overestimated or underesti- mated the marginal impact of rainfall on umbrella sales? Justify your answer.

2.[Total: 22 marks] Carol is interested in studying the housing market in Sydney. She considers the following regression 计量经济学final代做
ln(price) = α0 + α1 ln(income) + u; (3)
where price is the price of the house (in million dollars), and income is the annual income of the buyer as a household (in thousand dollars). We use natural logarithm throughout this question.
(a) [3 marks] Interpret the coecffcient α1.
(b) [4 marks] An extract of the ANOVA table is displayed below:

Compute R2and the adjusted ![]() .
.
(c) [6 marks] Based on the sample Carol collected, the estimated regression line is given by ln(d price) = 0:9 + 0:3 ln(income):
Little Bob, Carolís assistant, messed up with the data by mistakenly multiplying all observations (including all house prices and household incomes) by two. What will be the estimated regression line on the modified data? Show your steps that lead to your answer.
(d) To examine the geographic impact on house prices, Carol introduces a dummy variable north, which takes the value one if the house is located in northern Sydney, and zero otherwise. Using the original sample Carol collected (not the one modiÖed by Bob),the following regression was obtained:
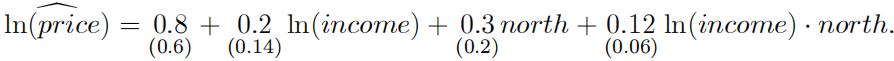
(4)
i.[4 marks]Suppose a homebuyer in northern Sydney earns an annual income of $200,000. What is the predicted house price according to regression (4)? Show your computation.
ii.[5 marks] Construct a 95% confidence interval of the coe¢ cient of the interaction term ln(income) north. Then, using the constructed confidence interval, test the following claim at the 5% significance level: ”The relationship between house price and household income is di§erent in northern region compared to the rest of Sydney.”
3.[Total: 20 marks] Bob is conducting a survey on whether customers were satisÖed with food delivery services. To this end, he collected a random sample of 50 customers with the following variables: 计量经济学final代做
- score : customer satisfaction score (over 0 to 5)
- dtime : delivery time (in minutes)
- ctime : cooking time (in minutes)
- atime = dtime + ctime
- bill : bill amount (in dollars)
Bob ran three di§erent regression models. The three models and selected outputs are displayed below.

Test the following claims at the 5% significance level. If the above information is insuffcient for you to test a claim, simply write ”insucffcient information” as the answer.
(a) [5 marks] ”Cooking time can a§ect the customer satisfaction score.”
(b) [5 marks] ”Delivery time and/or cooking time can a§ect the customer satisfaction
score.”
(c) [5 marks] ”Delivery time and cooking time have di§erent marginal impacts on the customer satisfaction score.”
(d) [5 marks] ”The bill amount can a§ect the customer satisfaction score.”

更多代写:加拿大微积分网课代修 托福家考保分 新加坡金融代上网课 summary essay 怎么写 出国留学论文代写 Behavioural Economics代考
