IT是什么?IT的全称就是Information Technology 即信息技术 基本概念和所指范围。那IT算法呢?顾名思义就是关于计算机的算法,例如最常使用的最短路径算法、二分查找算法等等。下面我们来看看计算机中有哪些比较重要的算法。
算法
简单来说,任何明确步骤或者用来解决特定问题的一系列步骤都可称为算法。那IT算法就是计算机中用来解决特定问题的的算法。算法必须具备以下3中重要特征:
有穷性。不会无限的执行,可以在有限次后终止。
确切性。每一个步骤都有确切的定义
可行性。可以在一定的时间内解决一定的问题。
那么下面我们来看看计算机中有什么重要的算法,有些算法在生活中造就了我们的生活以及现在的科技。
二分查找算法
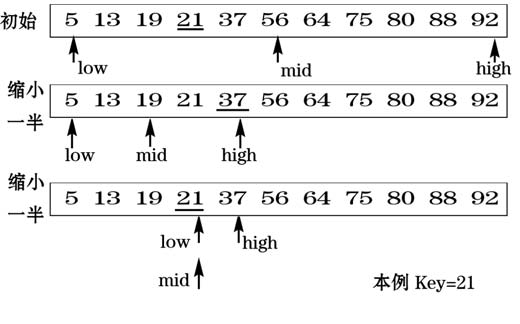
在有序数组中查找给出的元素。搜索的过程是从数组的中间元素开始,程序从中间元素查找,如果程序发现中间的元素与要查找的元素符合。那么久结束搜索,但是如果不相等久比较两者的大小,如果小于查找的元素就往小于中间元素的那一边开始,大于中间元素就反之。而且如果开始下一次的查找,和开始一样从中间的元素开始。直到得出结果。
数据压缩
通过减少计算机中所存储的数据或者通信传播中数据的冗余度,达到增大数据密度,使数据的存储空间减少的技术。这种技术在文件存储以及分布式系统领域中有十分广泛的应用。数据压缩也代表着尺寸媒介容量的增大和网络宽带的扩展。
A*搜素算法
也称为A星算法。这是一种在图形平面上,有多个节点的路径,求出最低通过成本的算法。和Dijkstra算法一样,可以找到一个最短路径。就相当于在一个游戏中你的角色站在一个地方,然后你鼠标点击另一个地方,就会算出最短路径。
归并算法
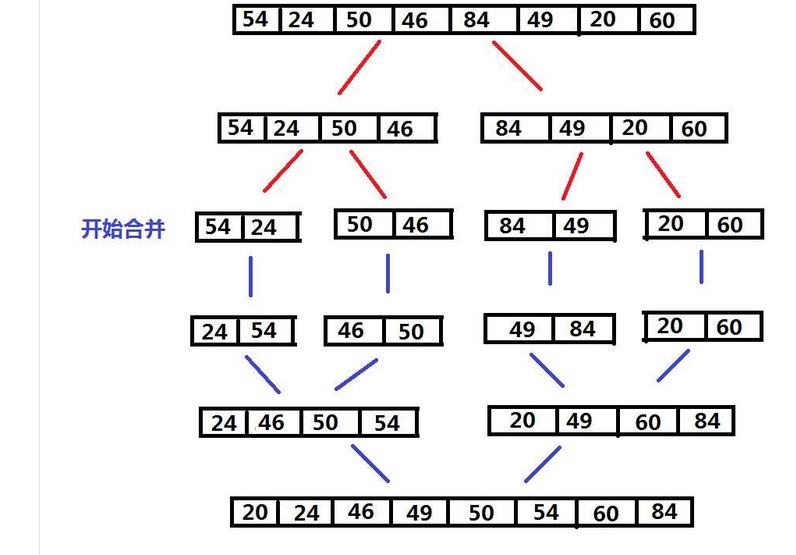
在计算机算法中是非常重要的一个,原理是把原始数组分成若干个子数组,对每一个子数组进行排序。然后把子数组与子数组合并,合并后进行排序,直到全部合并并且形成有序的数组。
快速排序算法
采用了分治思想,先在数组中取出一个数作为基准数,然后吧所有比这个大的放到右边,小的放在左边。然后在对左右区间进行同样的操作,知道左右区间只有一个数。但是不是很稳定,但是在处理随机列阵时效率相当高。
堆积算法
是指利用堆积树(堆)这种资料结构所设计的一种排序算法,可以利用数组的特点快速定位指定索引的元素。堆排序是不稳定的排序方法,辅助空间为O(1), 最坏时间复杂度为O(nlog2n) ,堆排序的堆序的平均性能较接近于最坏性能。
branch and bound(分支定界算法)
是一种在问题的解空间树上搜索问题的解的方法。但与回溯算法不同,分支定界算法采用广度优先或最小耗费优先的方法搜索解空间树,并且,在分支定界算法中,每一个活结点只有一次机会成为扩展结点。
Diffie–Hellman key exchange
迪菲-赫尔曼密钥交换(Diffie–Hellman key exchange,简称“D–H”) 是一种安全协议。 它可以让双方在完全没有对方任何预先信息的条件下通过不安全信道建立起一个密钥。这个密钥可以在后续的通讯中作为对称密钥来加密通讯内容。由于解释这种算法要用到很多的例子以及离散对数。所以有兴趣的朋友可以自行上网查找关于密钥交换算法。
Dijkstra(最短路径算法)
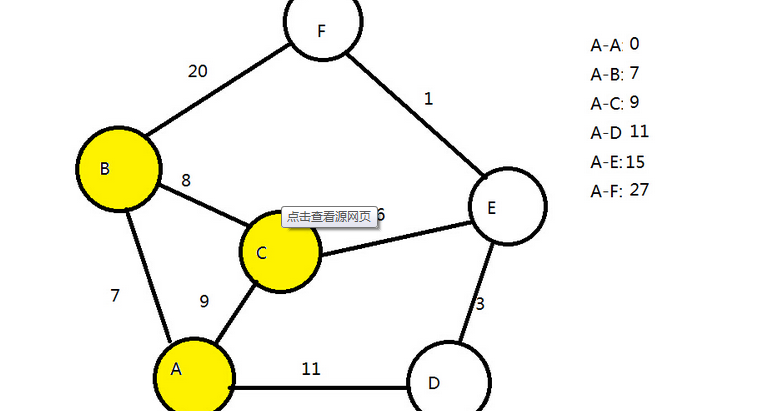
由荷兰计算机科学家艾兹格·迪科斯彻(Edsger Wybe Dijkstra)发明的。Dijkstra用于计算一个节点到其他所有节点的最短路径。主要特点是以起始点为中心向外层层扩展,直到扩展到终点为止。例如在一个地方有很多房屋,每一个房屋代表一个点,每个房屋间的距离都不相同。如果你这时要从一间屋子走到另一个屋子,但是你想走虽短路径,而Dijkstra就可以帮你找到最短路径。
动态规划
在数学和计算机科学中经常使用的算法。基本思想与分治法类似,也是将待求解的问题分解为若干个子问题(阶段),按顺序求解子阶段,前一子问题的解,为后一子问题的求解提供了有用的信息。在求解任一子问题时,列出各种可能的局部解,通过决策保留那些有可能达到最优的局部解,丢弃其他局部解。依次解决各子问题,最后一个子问题就是初始问题的解。
动态规划的思想是多种算法的基础,被广泛应用于计算机科学和工程领域。比较著名的应用实例有:求解最短路径问题,背包问题等。
欧几里得算法
#p#分页标题#e#
用于求出最大公约数的算法。辗转相除法首次出现于欧几里得的《几何原本》(第VII卷,命题i和ii)中,而在中国则可以追溯至东汉出现的《九章算术》。
最大期望算法
在统计计算中,最大期望(EM)算法是在概率(probabilistic)模型中寻找参数最大似然估计或者最大后验估计的算法,其中概率模型依赖于无法观测的隐藏变量(Latent Variable)。在机器学习以及计算机视觉的数据聚类领域会经常使用最大期望算法。
这个算法经过两个步骤进行计算:
第一步先计算期望,利用对隐藏的变量现有的估值,计算最大似然估计值。然后第二步就是最大化,最大化在第一步中求得的最大似然值来计算参数的值。第二步找到的参数有被用与下一次的第一步,不断地交替。
快速傅里叶变换(Fast Fourier Transform,FFT)
是离散傅里叶变换的快速算法,也可用于计算离散傅里叶变换的逆变换。快速傅里叶变换有广泛的应用,如数字信号处理、计算大整数乘法、求解偏微分方程等等。由于傅里叶变换的计算以及讲解很复杂,有兴趣的朋友可以自行上网查找。
Viterbi algorithm
寻找最可能的隐藏状态序列。
RANSAC

RANSAC(RANdom SAmpleConsensus)用于从一组观测数组中估计数学模型参数的迭代方法。RANSAC算法的输入是一组观测数据(往往含有较大的噪声或无效点),一个用于解释观测数据的参数化模型以及一些可信的参数。RANSAC通过反复选择数据中的一组随机子集来达成目标。它是一种非确定性的方法,因为他只能用一定的概率得到合理的结果。但是随着迭代的次数增加,概率也会增加。
并查集Union-find
这是一种数型的数据结构。是一种非常精巧而实用的数据结构,它主要用于处理一些不相交集合的合并问题。一些常见的用途有求连通子图、求最小生成树的 Kruskal 算法和求最近公共祖先(Least Common Ancestors, LCA)等。
算法无论在计算机科学中还是在数学中都有着不可取代的位置,可以说没有这些算法现代计算机科学就不可能快速发展。文中的只是算法中的重要的一部分。如果你对文中的算法想深入了解,你可以在网上查找深层的解析,在这里只是向大家介绍这些算法的概念以及思想。
