Computer Science代写 Computing代写 Assignment代写 Homework代写

ftopics in Computer Science: Probability & Computing

Computer Science代写 Consider a graph H in G(n, p).(a)If f (H) is the random variable that counts the number of isolated vertices

CMP_SC 7001, Fall 2019

Instructor: Petros Valettas Homework Assignment 3 Due date: Monday, December 9

1. Consider a graph Hin G(n, p).

(a)If f (H) is the random variable that counts the number of isolated vertices (i.e. vertices of degree 0)  in  H,  show  that E[ f (H)] = n(1 – p)n–1.

(b)Showthe following threshold behavior: For ” 2 (0, 1) we have that

i. if p > (1 + “)^log n, then

lim P(H G(n, p) : f (H) 1) = 0,

if p < (1 – “)^log n, then

ii. lim P(H G(n, p) : f (H) 1) = 1.

Hint; you may use the second moment method.

2.Solve MU:16. Computer Science代写

3.Letb₁,. .., b_N be sequences of n-bits, e. b_i = (b_i1,. .., b_in), where b_ij 2 {0, 1} for i = 1, 2,. .., N.

(a)Show that there exists J ✓ [n] := {1,. .., n} suchthat

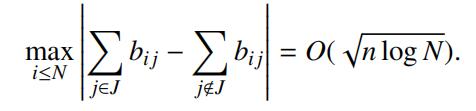
Hint; Consider the N ⇥ n matrix B with rows b_i, i N. Note that the above estimate can be written as kBxk₁ =  O(    n log N),  where  x =  (x₁,. .., x_n)  2 {–1, 1}   and  J  =  { j      n  :  x _j =  1}.   Choose  independently  and uniformly  at  random  n signs  x_i 2 {–1, 1} and  consider  the  probability  P(kBxk₁ > t) for  appropriate  t  > 0.   See [MU, Section 4.4].Computer Science代写

(b)Showthat the above estimate is optimal up to logarithmic terms: There is an n ⇥ n matrix M with 0-1 entries such that

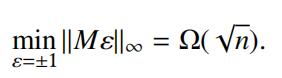
Hint; fix a vector ” with 1 coordinates. Use the probabilistic method to construct a matrix  M by sampling the  entries independently and uniformly from {0, 1}. Show that P(kM“k₁ < c pn) ⌧ 2–n. See [MU, Exercise 6.16].

4. Relative and Conditional entropy. Let P, Q be two probability functions on some finite sample space⌦ =   !₁,. .., !_n .  We write Q  P if  p_i = 0 implies q_i = 0.  The relative entropy of Q and P is defined by

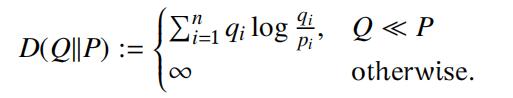
(a)Showthat D(Q||P) ≤ 0 and D(Q||P) = 0 if and only if Q = P.

(b)IfP is the uniform distribution on ⌦, then D(Q||P) = log |⌦| – H(X).1

(c)Showthat the Shannon entropy H(X) satisfies 0 H(X) log |⌦|.Computer Science代写

Hint; the function u 7! u log u is convex.

(d)Let(X, Y) be a pair of (discrete) random  Then, the entropy of the pair H(X, Y) satisfies

H(X, Y) H(X) + H(Y),

with equality if and only if X, Y are independent.

Hint; you may want to write H(X) + H(Y) – H(X, Y) as the relative entropy of the joint distribution of (X, Y) with another one. What is that?

5.Let P, Q be two distributions on  a  finite  set  ⌦.  We  define  the  total variation distance  between the distributions by Computer Science代写

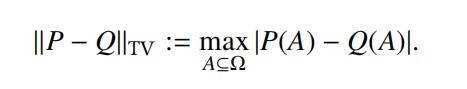
(a)Showthe following alternative expression:

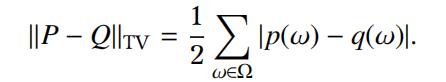
(b)Show that for any random variable X : ⌦ ! R wehave

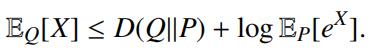
Hint; you may want to use the numerical inequality xy y log y – y + ex for y > 0 and x 2 R. Apply the latter for x = log( exi ) and y = q /p for i = 1, 2,. .., n.

(c)Use  the  previous  inequality  for  X= h(Y E_P[Y]), where h > 0 and Y is an appropriate Boolean random variable on ⌦.Computer Science代写

Hint; note that there exists a set A⇤ ✓ ⌦ such that kQ – Pk_TV = Q(A⇤) – P(A⇤) = E_Q[Y – E_P[Y]]. What is Y?

(d)UseHoeffding’s lemma for Y in order to derive the following inequality:

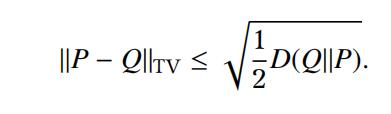
1Note that here we consider the Shannon entropy with log instead of log2.

更多其他：计算机代写 lab代写 python代写 作业代写 code代写  homework代写 加拿大代写 C++代写 金融代写 matlab代写 算法代写 assignment代写

合作平台：天才代写 幽灵代写 写手招聘 Essay代写