CSC 236H1 Sample Term Test
计算机理论导论代考 You are expected to submit your work on MarkUs after 70 minutes, NOT 85. Submissions will NOT be accepted 85 minutes after you begin,
Duration — 70 minutes for writing the test
15 minutes for uploading and submitting to MarkUs
You are expected to submit your work on MarkUs after 70 minutes, NOT 85. Submissions will NOT be accepted 85 minutes after you begin, except for a short 5-minute period during which any submission will be penalized by -2% for every additional minute of lateness.
The questions in this sample test and their solutions have been collected from tests and exams of past offerings of the course. 计算机理论导论代考
Therefore, the style and approaches used in the sample solutions might slightly be different than what we did in class.
IMPORTANT NOTE: One of the key factors in a test is time pressure. You may be able to answer a question when you have an extended amount of time, but not within the time limit the examiner expects. The followings are the time expectations that designers of the questions in this sample test had in mind:
Q1: 15 min
Q2: 15 min
Q3: 20 min
Q4: 15 min
When answering the questions time yourself! If you cannot complete a question within the corresponding time limit it means that you are not prepared yet and need to practice more.
Good Luck!
Question 0. [0 mark] 计算机理论导论代考
Write your answer to this question either in a typed document or on a piece of paper, depending on what your plan is for writing the test, and submit it. This will give you practice with this method of submitting your answers, in case you need to use it during the test. Better to figure it out now, when it doesn’t count!
Remember that the purpose of the real test will be to assess your understanding of the course material. If your goal is to learn this material, because you understand that it will be useful in your future studies and work, then you should welcome the opportunity to find out how you are doing. This will provide you with essential feedback to help you improve your own learning.
In this context, we need to see what you can do. Otherwise, any feedback we provide will be meaningless and you will miss an opportunity to improve yourself. For this reason, we expect you to answer the real test questions using only the aids allowed and NOT to try to find answers by any means other than your own individual efforts.
On the real test, we will ask you to submit an Academic Integrity statement like the one below. 计算机理论导论代考
By signing this Statement, I am attesting to the fact that I, [name] , [student number] , have abided fully by the Code of Behaviour on Academic Matters. I have not committed academic misconduct and I am aware of the penalties that may be imposed if I have committed an academic offence.
For this practice test, please write the statement on a piece of paper and send it in. You don’t need to sign it or include your student number, but this way it will be ready for the actual test. (While you’re at it, it might be a good idea to take the opportunity to find out about the Code of Behaviour and the possible sanctions that can be imposed if you are suspected of committing an academic offence.)
Question 1. [0 mark] 计算机理论导论代考
Using the Well-Ordering Principle, prove that 2n < n! for all n ∈ N,n ≥ 4.
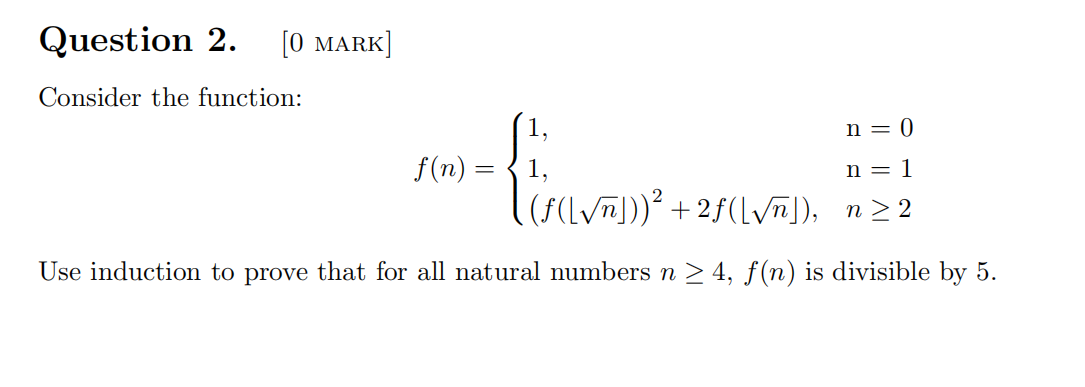
Question 3. [0 mark]
Consider the following recursive definition of binary trees.
- The empty tree (that contains no node and no edge) is a binary tree.
- If T1and T2are binary trees and r is a single node, then the tree obtained by making T1 the left subtree of r and T2 the right subtree of r is also a binary tree. (This is illustrated on the right.)
- Nothing else is a binary tree.
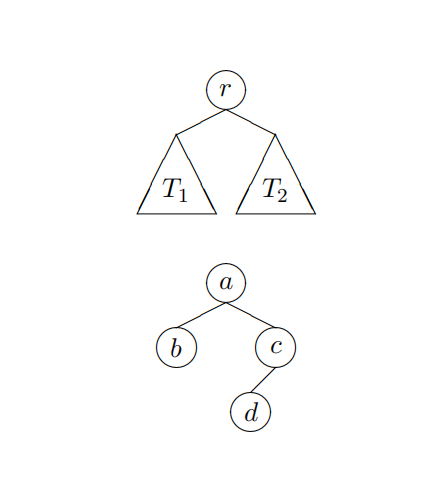
A path is a sequence of nodes with edges between them. For example, “b—a—c—d” is a path between b and d in the binary tree pictured on the right. A sequence with just one node (like “c”) is a valid path, and so is the empty sequence “ ” (vacuously).
Use structural induction to prove that for all binary trees T, there is a unique path between any two nodes of T.
Question 4. [0 mark] 计算机理论导论代考
Let L = {w ∈ {0, 1}∗: |w| is odd and w contains at least one 0}.
Construct a DFA that accepts L.
It is possible to give a correct DFA with 4 states. One mark will be deducted for each extra state that your DFA uses.
Provide appropriate state invariants for your DFA.
Do not use regular expressions in your state invariants.

