英文数学作业代写 Math 135A代写

Math 135A: HW4

Due Friday, February 26

英文数学作业代写 Consider a random walk  on the integer lattice  Z.  At  each  unit time step the walkertakes  one step  to the left or one step to the right.

1.Let X₁, X₂, and X₃denote continuous random variables with joint density function f_X1,X2 ,X3 . That is   英文数学作业代写

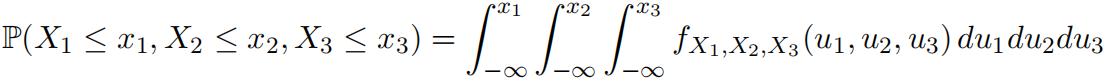
Defifine

Y₁ := X₁, Y₂ := X₁X₂, Y₃ = X₁X₂X₃.

a)Find the joint density function for Y₁, Y₂, andY₃.

b)AssumeX₁, X₂, and X₃ are independent and uniformly distributed on [0, 1]. Find the densityfunction for Y₃. Verify that your result implies E(Y₃) = 1/8 (why is this easy to see without computing the density function of Y₃?)

2.Consider a random walk  on the integer lattice  Z. 英文数学作业代写

At  each  unit time step the walkertakes  one step  to the left or one step to the right. If the walker is at  an even  numbered lattice  site,  the probability  of one step to the right is p_e and one step to the left is q_e := 1 − p_e. Similarly, if the walker is at an  odd numbered lattice site,  the probability  of one step  to the right  is p_o  and one step  to the left  is  q_o := 1 − p_o.  Let T ^e  denote the time for the first passage to the site +1 given  that the walker  startsat the side  Let T ^o denote the first passage time to the site +2 given that the walker starts at the site +1.

Introduce the generating functions

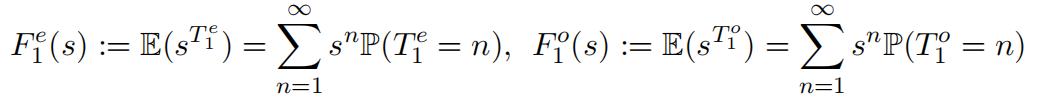
a)Show that F ^eand F ^o satisfy the equations

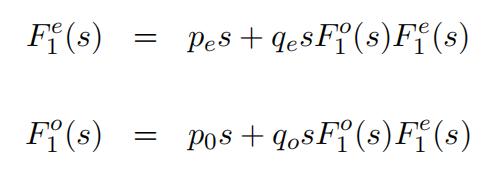
b)Fromthe above equations derive a quadratic equation for F ^e(s). Solve your equation for F ^e(s).I got the result

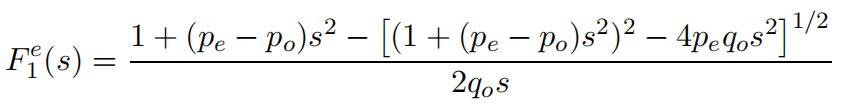
Note the algebraic identity p_eq_o − p_oq_e = p_e − p_o. Note that when p_e = p_o = p the above result reduces to  英文数学作业代写

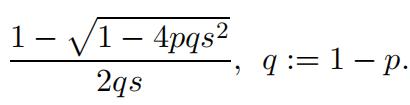
which was derived in class.

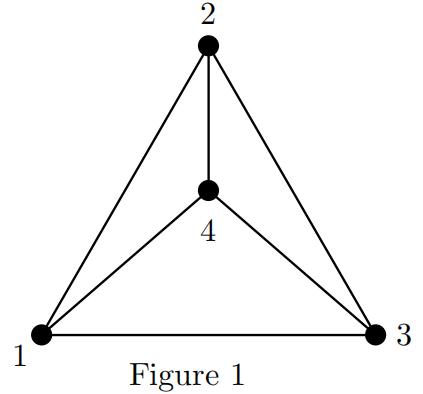
3.Arandom walk in discrete time is performed on the graph shown in Figure  From each vertex the walker is equally likely to choose one of the neighbors connected by a bond. 英文数学作业代写

Using the labelling in the figure, write down the transition matrix P . Find the invariant measure π; that is, the probability measure that satisfies π · P = π.

4.The cumulant generating function K_X(s) of the random variable X is defined by 文数学作业代写

K_X (s) = log(E(e^sX))

Assuming that K_X has a convergent Taylor expansion

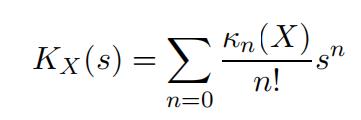
the κ_n(X) is called the nth cummulant of X.

a)Express κ₁(X), κ₂(X), and κ₃(X) in terms of the moments of X.

b)Let X be normally distributed with mean zero and variance 1, find the cumulants of X. Hint: First find an expression for E(s^X) and then take the logarithm.

c)Suppose X and Y are independent random variables. Showthat

κ_n(X + Y ) = κ_n(X) + κ_n(Y ).

更多代写：新加坡Cs网课代写 新加坡EconFinal exam代考 英文科技留学essay代写 英文report代写 英文Paper代写 美国统计代写

合作平台：essay代写 论文代写 写手招聘 英国留学生代写