英国统计代考 Probability代写

STATISTICS

Probability: Theory and Applications

(Time allowed: 24 Hours)

英国统计代考 This assessment is open book, you are permitted to refer to your lecture notes and other course materials, including online resources.

This Final Assessment has been designed so that a well-prepared student could com- plete it within 2 hours. You are allowed spend longer without penalty, as long as submitted before the deadline.
Submitsolutions online via Canvas by 13:00, Saturday, June 27th (NZ time)
Itis your responsibility to ensure your assessment is successfully submitted on It is recommended that you aim submit well in advance of the deadline, in case of any technical issues. You are also advised to download your submitted PDF document from Canvas to verify that it uploaded correctly. 英国统计代考
This assessment is open book, you are permitted to refer to your lecture notes and other course materials, including online resources.
Allsubmitted work must be your You must NOT discuss it with anyone else.
There are a maximum of 60 marks
Each question is worth 20 marks. You may answer as many questions as you like, but ONLY your best three questions will count towards your final mark.
For full marks you must use good notation, show calculations, justify your steps, state any general results to which you appeal, and simplify answers appropriately.
Calculators are permitted (but notrequired).

Support: 英国统计代考

If you have any concerns regarding your Final Assessment, please call the Contact Centre for advice, rather than your instructors.

–TheContact Centre can be reached on these numbers:

– Auckland: 09 373 7513

–Outside Auckland: 0800 61 6263 英国统计代考

–International: +64 9 3737513

Forany Canvas issues, please use 24/7 help on Canvas by chat or phone.
If any corrections are announced during the 24 hours of the final assessment, you will be notified by a Canvas Announcement. Please ensure your Canvas notifications are turned on during this period.

Question Interpretation: 英国统计代考

Please note that during the final assessment period you cannot contact your instruc- tors for clarification on how to interpret the wording of any specific questions or to verify that your answer is correct. Interpreting wording and making appropriate assumptions is part of what is being assessed. You will need to interpret the question yourself and check your own answers. 英国统计代考

If you believe there is a typo, first re-read the question to check you have not mis- understood the question, as it is very common to misread questions. If you still believe there is a typo, please phone the Contact Centre.

Academic Honesty Declaration:

By completing this assessment, you agree to the following declaration:

I understand the University expects all students to complete coursework with in- tegrity and honesty. I promise to complete all online assessment with the same academic integrity standards and values. Any identified form of poor academic practice or academic misconduct will be followed up and may result in disciplinary action.

As a member of the University’s student body, I will complete this assessment in a fair, honest, responsible and trustworthy manner. This means that:

I declare that this assessment is my own work.
I will not seek out any unauthorised help in completing this assessment.
I am aware the University of Auckland may use plagiarism detection tools to check my content.
I will not discuss the content of the assessment with anyone else in any form, including, Canvas, Piazza, Facebook, Twitter or any other social media or online platform within the assessment period. 英国统计代考
I will not reproduce the content of this assessment anywhere in any form at any time.
I declare that I generated the calculations and data in this assessment indepen- dently, using only the tools and resources defined for use in this assessment.
I will not share or distribute any tools or resources I developed for completing this assessment.

Considera Random Walk (RW) between neighbouring vertices of the infinite binary tree whose structure can be indicated pictorially, at least up to the first few levels, by the following picture:

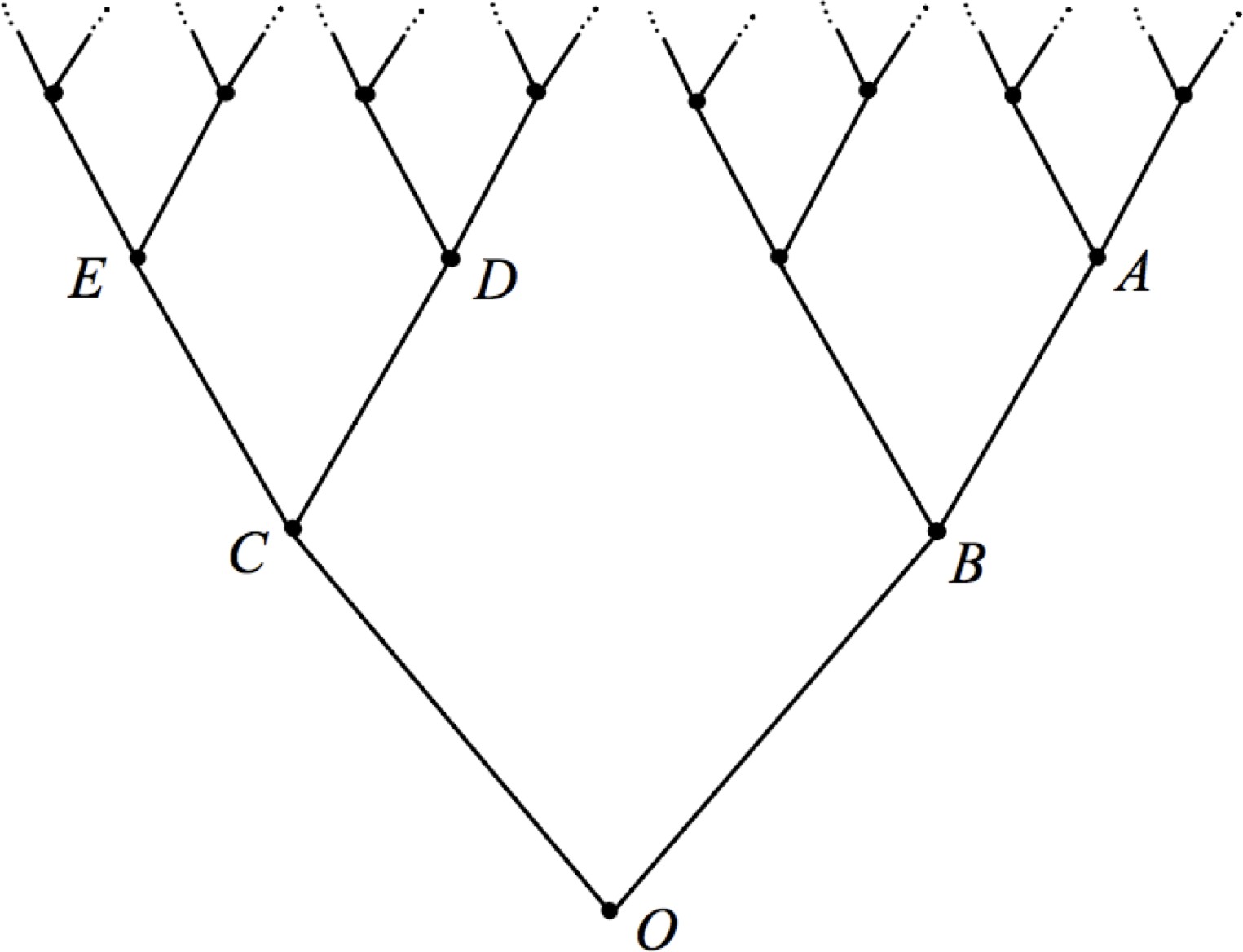
If the RW is currently at vertex O, it is equally likely to move to either vertex C or vertex B at the next time step, independently of the past. Otherwise, if the RW is currently at some other vertex v then, independent of the past, on its next step it will move to vertex w with probability 1/3 if and only if v and w are neighbouring vertices. For example, from C the RW is equally likely to move to D, E or O at the next time step.

Let P_w represent the probability law of the RW when initially started at some vertexw.DefineT_w to be the time the RW first hits vertex w, where T_w = 0 if the RW

is initially started at vertex w and T_w = +∞ if the RW never hits vertex w at any non-negative time. As usual, define P(F ; G) := P(F ∩ G) for any events F and G.

The shrinking size of branches in the diagram is only to permit easy drawing; distances in the picture are not important for the RW, only the neighbourhood structure between vertices is significant. For example, by symmetry, P_B(T_O < ∞)

will have the same value as P_E(T_C < ∞). 英国统计代考

Show that

(a) P_C(T_O < ∞) = ¹ , [8]

(b) P_O(T_C < ∞) = ² , [4]

(d) P_C(T_D < ∞ ; T_E < ∞) = ¹⁸ . [4]

2.Considera discrete time branching process Z = (Z_n)_n_≥₀ with Z₀ = 1, where Z_n

represents the number of individuals in a population at time n. At time n + 1, each

individual in the n^th generation is replaced by a random number of new individuals, each distributed like an independent copy of some offspring random variable, X, taking values in {0, 1, 2, . . . } and satisfying µ := E(X) < ∞.

Define the probability generating function (PGF) of the offspring distribution X by

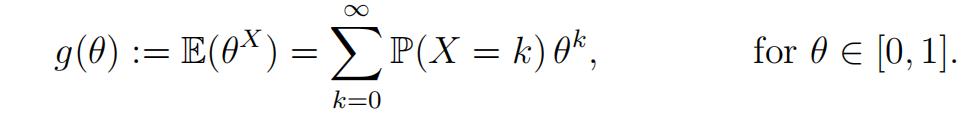
(a)Calculate E(θ^Zn+1 Z_n= k) in terms of g(θ) and k, hence deduce an expres- sion for E(θ^Zn+1 Z_n). Explain the fundamental difference between these two conditional [3]

(b)Definethe PGF for Z_n as g_n(θ) := E(θ^Zn ). Prove that g_n₊₁(θ) = g_n(g(θ)). 英国统计代考

Deduce an expression for g_n(θ) depending only on g, θ, and n. [2]

For the remainder of this question, consider the special case when the offspring random variable, X, satisfies

P(X = k) = (1/2)^k⁺¹ (k = 0, 1, 2, . . . ).

(c)Show that g(θ) = 1/(2 − θ) and that g^j(1)= [2]

(d)Writedown g₀(θ) and g₁(θ). Prove by induction that, for all n ∈ {0, 1, 2, . . . },

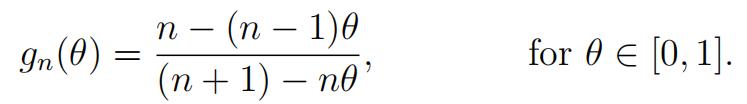[5]

(e)Deduce that P(Z_n= 0) = n/(n + 1). Hence, prove that the population will eventually become extinct, almost [3]

(f)Byexpanding g_n(θ) as a power series in θ, determine P(Z_n = k) for k ≥ [5]

3.Let Z be a Poisson random variable (RV) of parameter µ > 0,written Z P o(µ), so that 英国统计代考

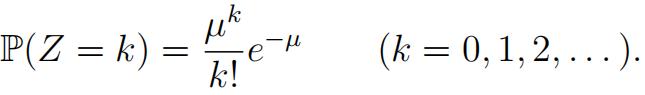
Suppose X₀, X₁, . . . is a sequence of independent random variables such that, for each i ≥ 0, X_i is a Poisson RV of parameter λ_i, where

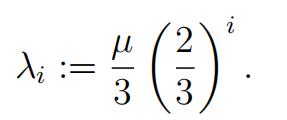µ .2 Σ_i

(a)Calculatethe probability generating function (PGF) of Z,

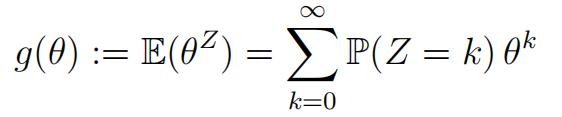
where θ ∈ [0, 1]. [2]

(b)Writedown the PGF of X_i, g_i(θ) := E(θ^Xi ). [1]

(c)Define Y_n:= Σn X_i. Find the PGF of Y_n, h_n(θ) := E(θ^Yn ). Hence, deduce

that Y_n is a Poisson RV with rate parameter µ(1 − (2/3)ⁿ⁺¹). Hint: Recall that 1 + x + x² + · · · + xⁿ = (1 − xⁿ⁺¹)/(1 − x) for x ƒ= 1. [3] 英国统计代考

(d)Forθ ∈ [0, 1], show that h_n(θ) → e^µ⁽^θ⁻¹⁾ as n → ∞. Stating any general result that you appeal to, deduce that Y_n converges in distribution to Z, that is,

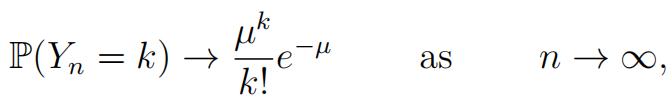
for each k ∈ {0, 1, 2, . . . }. [2]

(e)DefineY := ^∞i=0 X_i. Use continuity of probability (or monotone convergence) to prove that P(Y_n ≤ k) → P(Y ≤ k). Deduce that Y ∼ P o(µ). [2]

(f)Deducethat Y Y_n = ^∞i=n+1 X_i P o(γ_n) for some parameter γ_n that you should calculate and Hence, show that 英国统计代考

(i) E(|Y − Y_n|) → 0 as n → ∞,

(ii) Y_n → Y in probability. [6]

(g)Stating any general result to which you appeal, show that, with probability one,only finitely many of the events {X₀ ≥ 1}, {X₁ ≥ 1}, {X₂ ≥ 1}, . . .

Deduce that Y_n → Y almost surely. [4]

4.Recallthat a Poisson point process on G ⊂ Rn with intensity function λ : G → 英国统计代考

[0, ∞) is a random collection of points in G such that:

(P1) if G₁, G₂, . . . are disjoint subsets of G, then the numbers N (G₁), N (G₂), . . .

of points occurring in G₁, G₂, . . . are independent random variables;

(P2) N (G_k) has the Poisson distribution of parameter x∈ttk λ(x)dx.

(a)Letν, µ > An experiment is performed where Red and Blue particles hit a sensor at random. Suppose that the positions where Red particle hit the sensor form a Poisson point process on R2 of constant intensity ν. Suppose that the positions where Blue particle hit the sensor form a Poisson point process on R2 of constant intensity µ. In addition, suppose that the positions where Red and Blue particles hit are independent.

i.Describe,with reasons, the combined process for the positions of all par- ticles (ie. regardless of whether Red or Blue) hitting the [2]

ii.Findthe distribution of the distance, Z, from the origin to the closest particle. [2]

iii.What’s the probability the two particles that are closest to the origin consistof one of each colour? [3] 英国统计代考

iv.Given that exactly four Red particles hit the sensor inside the square shaped region S = [ 2, +2]², explain why U has conditional probability densityfunction

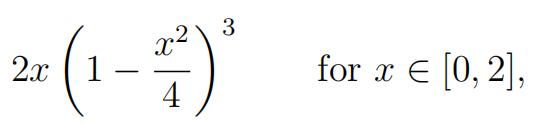
where U := inf{x > 0 : at least one Red particle hit within [−x, x]2}.

Hint: You should recall and use the ‘conditional uniformity’ principle. [4]

(b) Let u, v > 0. Suppose that N is a Poisson point process on (0,∞) with

intensity function λ(s) = 1/(s(1 + s)). 英国统计代考

(i) Show that the probability no points of N occur in the interval (u, v] is u

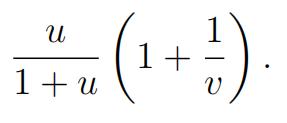
Hint: Use partial fractions and recall that (ln x)0 = 1/x. [4]

(ii) Write down the probability distribution and mean for the number of points

of N occurring in the interval (u, v].[2]

(iii) Do fifinitely or infifinitely many points occur in the interval (u, ∞)? Brieflfly

explain your answer.[3]

合作平台：essay代写论文代写写手招聘英国留学生代写