MAT301 Final Assessment
due Monday August 24
英国数学代考 Each positive-numbered problem is worth 10 points, for a total of 60. If you do not solve problem 0 completely, you will get 0 on the test.
Instructions 英国数学代考
The test has 12+1 problems. You must submit 6+1 solutions, choosing:
- problem 0 (not achoice)
- 3 homework-styleproblems:
– one of 1,2
– one of 3,4
– one of 5, 6,7
- 2 discussionquestions:
– two of 8, 9, 10
- 1 project-relatedproblem:
– one of 11, 12
Each positive-numbered problem is worth 10 points, for a total of 60. If you do not solve problem 0 completely, you will get 0 on the test.
Most of the problems are split up into short steps. Each step requires just one key insight or a brief computation. You are allowed to skip a part of a problem and use it freely in the sequel.英国数学代考
Among the positive-numbered problems you choose to submit, you do not have to answer everything to get a good score. To encourage you to do the longer problems (2, 3, 5–7, 11) we’ll mark them just up to 10 points even though they have more than 10 parts.
You must justify your answers (with proof or citation) to receive full credit. Citations can only come from our course materials (notes, slides, homework, quizzes, glossary, Piazza); everything else you must prove.
While this exam is take-home and open-book, it is also individual. “Take- home” means you have an extended period of time to complete it (in our case, 5 calendar days). “Open-book” means you’re allowed to access pre-existing 英国数学代考
materials (created before the start of the exam) for assistance (e.g. your notes, our notes, textbooks, static online resources). “Individual” means you do it on your own: do not collaborate with others nor ask others for help, neither online nor offline.
Problem 0. 英国数学代考
a)Whatdoes “take-home” mean?
b)Whatdoes “open-book” mean?
c)What does “individual”mean?
d)Reproducethe following statement in your finest handwriting and sign it with your autograph.
I vow to complete this exam individually, neither accessing nor requesting access to any unauthorized aid, and neither providing assistance to nor seeking assistance from any other individual.
Upload a picture of your solution to this problem with your student card placed face-up somewhere on the page, neither obscured nor obscuring.1 英国数学代考
1If you don’t have your student card, write your student number on the page with a note explaining where your student card is.
Part 1. Homework-style problems
Problem 1. Let C be the circle x2 + y2 = 1 and let O be the point (1, 0).
a)Findan explicit formula for P Q in terms of the Cartesian coordinates of P and Q.
b)Whatis the ⊕-inverse of (x, y) in C?
c)Showthat ι(x, y) = x + iy is an embedding of C into C×. What is im ι? 英国数学代考
d)Useangle-addition formulas to show that τ (θ) = (cos θ, sin θ) is an epimorphism R ‹ C.
e)LetL = R ∪ {∞} be the group from Homework Complete the definition of σ(x, y) = y/x so that σ becomes a homomorphism C → L.
f)What are im σ and kerσ?
g)Show that στ = tan. Immediately deduce the angle-addition law for tangents.
Problem 2 (Continuation of Homework 6 Problem 3). 英国数学代考
We showed that G is cyclic if k = 2. Suppose k > 2.
f)Show that k =3
g)Show that p = n +2
Let x1, x2, x3 be representatives for the pivot-orbits and let si = o(Stabtt(xi)).
h)Usethe definition of pivots to show that si > 1 for all i.
i)Use the Orbit–Stabilizer theorem to showthat Σ3 s−1 >
j)Assume w.l.o.g. that s1™ s2 ™ s3. Show s1 = 2 and s2 = 2 or
k)Listall triples (s1, s2, s3) satisfying the conditions in parts h–j) 英国数学代考
l)For each triple you listed, what is the corresponding value ofn?
m)By considering axes of rotation, explain why can’t G be Supposes1 = s2 = 2 and let s = s3 “ 2. We will show that G is dihedral.
Supposes = Show that G ∼= D2.
n)Suppose s > 2 and let H = Stabtt(x3).
o)Showthat the only pivots of H are x3 and −x3. Conclude that H ∼= Cs.
p)Show that −x3∈ Orbtt(x3) by eliminating the
q)Pick g in G such that g(x3) = −x3. Show that g has order
r)Let h ∈ H. Show that gh has order
s)Concludethat G ∼= Ds.
Problem 3. 英国数学代考
In his Memoir on the Theory of Mathematical Form of 1886,
A.B.Kempe listed all 5 groups of order 12—or so he thought! As Cayley pointed out 4 yearslater,
For the order 12, Mr. Kempe has five groups, but one of these is non-existent, and there is a group omitted; the number is thus = 5.
Here was Kempe’s “group”, given as permutations of the 12 letters a, b, c,
…, l:

First, you will verify Cayley’s claim that Kempe’s “group” is not a group.
a)The ith row defines a permutation σiof the first row. For example,
σ = a b c d e f g h i j k l . b a d c j i l k f e h g
Write each σi as a product of disjoint cycles.
b)Compute o(σi) for eachi.
c)Show that Kempe’s group is not closed under 英国数学代考
d)Showthat Kempe’s group is not closed under
e)Usethe totient function to give another reason why Kempe’s group is not a
Next, you will look at the subgroup generated by Kempe’s group. Let T =(σ1, . . . , σ12) ≤ Sym({a, . . . , l}).
f)Write out all 12 elements of C= (σ7).
g)Which σi’s are inC?
h)Show that σiCσ−1= C for all i.
i)Deduce that C Ð T.
j)Let K = (σ2). Show that CK ≤ T.
k)Show that σi∈ CK for all i.
l)Deduce that T = CK. What is o(T)?
Problem 4 (Continuation of Homework 6 Problem 2). 英国数学代考
We found a monomorphism Φ : S5 ‹→ S6. Let H be its image. Then S5 ∼= H
so [S6 : H] = 6!/5! = 6.
Consider the action of S6 on the coset space S6/H by left multiplication, and let Ψ be the composition of the associated permutation representation S6 → Sym(S6/H) and the isomorphism Sym(S6/H) −∼→ S6.
e)Show that f is a homomorphism.
f)Use part e) to show that fis injective.
g)Show that Ψ is an isomorphism.
h)Show that σ and τ have the same cycle type iff Ψ(σ) and Ψ(τ ) have the same cycle type. 英国数学代考
i)Conclude that Ψ sents conjugacy classes to conjugacy classes.
j)Explain why H contains an element σ of the form (a b)(c d)(ef ).
k)Usethe coset action to show that Ψ(σ) has at least one fixed point.
l)Whatis the cycle type of Ψ(σ)?
m)Is Ψ an innerautomorphism?
Problem 5.
The Cayley number of a finite group G, denoted π(G), is the least n “ 0 such that G ‹→ Sn. (Note that S0 is the trivial group.)
a)Show that π(G) ™o(G).
b)Showthat π(G) = 0 if G is trivial, otherwise π(G) > 2.
c)Suppose o(G) > Let m be the greatest integer such that m! < o(G). Prove that π(G) >m. 英国数学代考
d)Usec) to compute π(Sn) for all n > 1.
e)Usec) to compute π(An) for all n > 2.
f)Showthat if G ‹→ H then π(G) ™ π(H), with equality if G ∼= H.
g)Show that Sn× Sm ‹→ Sn+m.
h)Given G ‹→ Snand H ‹→ Sm, construct an embedding G × H ‹→ Sn × Sm.
i)Deduce that π(G × H) ™ π(G) +π(H).
j)Letp be a prime number and let k be a positive Suppose Sn has an element of order pk. Show that n “ pk. 英国数学代考
k)Deduce that π(Cpk ) =pk.
l)Givean upper bound for π(Cn) in terms of the prime factorization of n.
m)Compute π(Ck) for as many k “ 1 as you can.
Problem 6. 英国数学代考
Let G be a group and let x G. An element conjugate to its inverse is called heavy, otherwise light.
a)Show that e is heavy.
b)Show that involutions are heavy.
c)Showthat if x is heavy, then every conjugate of x is heavy.
A conjugacy class with only heavy members is heavy, while a conjugacy class with only light members is light. 英国数学代考
d)Prove that every conjugacy class is either heavy or light. Assumehenceforth that G is finite of order n and has class number k.
e)Provethat the number of light conjugacy classes is even.
f)Let k1be the number of heavy conjugacy classes and let k2 be half the number of light ones. What is k1 + 2k2?
g)Suppose G is abelian. Show that k1= 1 + ϕtt(2).
h)Suppose G is dihedral. Show that k2= 0.
The mass of G is the number
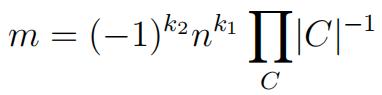
where the product is taken over the heavy classes only.
i)Prove that m is an
j)Prove that n dividesm.
k)If G is abelian and n is odd, what is m? 英国数学代考
l)Compute the masses of the cyclic groups Csfor all s “
m)Compute the masses of the dihedral groups Dsfor all s “
Your answers to k) and l) should depend on n and s (mod 4) and your answer to m) should depend on s (mod 2).
Problem 7.
Let G be a finite group of order n. For each integer a define the function πa : G → G by πa(x) = xa for all a in G.
a)What are π0and π1?
b)Completethefollowing table in the special case G = D4.
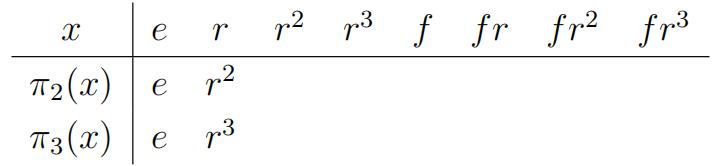
Returning to the general case, let a, b ∈ Z.
c)Prove that πa(x)πb(x) = πa+b(x) for all x inG.
d)Prove that πa(πb(x)) = πab(x) for all x inG. 英国数学代考
e)Supposea ≡ b (mod n). Prove that πa(x) = πb(x) for all x in G.
f)Supposegcd(a, n) = Use B´ezout’s identity to show πa is bijective.
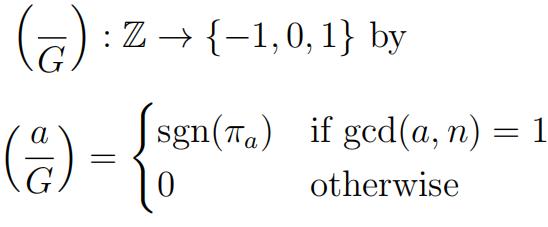
Define the G-symbol
where sgn denotes the sign of a permutation.
g)Whatare 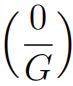 and
and 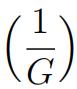 ?
?
h)What are 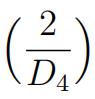 and
and 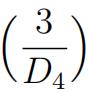 ?
?
i)By considering two cases for gcd(ab, n) provethat 英国数学代考
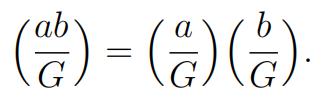
j)Suppose a ≡ b (mod n). Provethat
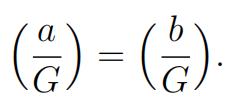
k)Evaluate the D4-symbol for every a inZ.
Part 2: Discussion questions
The questions in this Part are meant to get you thinking about the big picture. Write whatever you deem is relevant, but remember to:
- staywithin the scope of our course, and
- communicate your thoughts clearly and
You must justify (with proofs) or cite (with course materials) all your claims.
Problem 8.
The three most important families of groups are the cyclic, the dihedral, and the symmetric groups. Explain, in words, what these groups are. Devote one paragraph to each group, making sure to address:
- how the group iswritten,
- how its elements arewritten, 英国数学代考
- the order of thegroup,
- the orders of its elements,and
- its subgroups.
Problem 9. 英国数学代考
Equivalence relations have played a fundamental role in our course. Define each of the following equivalence relations and discuss their applications. Which of them are special cases of others, and how?
- congruence modulon
- theleft coset relation
- theunnamed relation on G[d] (Lecture 7)
- theorbits of a permutation (Lecture 10)
- the orbits of a group action (Lecture16)
Problem 10.
Throughout MAT301 we made repeated use of a small number of important proof techniques:
- counting viapartitions 英国数学代考
- reducing modulop
- decomposition
- division withremainder
- rewriting theidentity
How did these phenomena arise in the proofs in our course? Give two exam- ples for each one.
Part 3: Project-related problems 英国数学代考
Problem 11. Consider this passage.2
- Lemma II. – Let p be a prime number; pfthe highest power of p that dividesthe product 1 · 2 · 3 · · · k: one may construct a group of substitutions of order p on k letters.
If k < p, we have f = 0, pf = 1, and the group formed of the sole substitution 1 will satisfy the question. 英国数学代考
We will show that if the proposition is true for every number inferior to pν, then it will be so for every number inferior to pν+1.
Any integer k not inferior to pν and inferior to pν+1 can be put in the form k = qp + r, q being < pν and r < p. Among the k given letters, let’s consider qp of them and repartition them into q systems a, b, c, . . . , a1, b1, c1, . . . , each containing p letters.
Let S be the substitution which circularly permutes a, b, c, . . . without displac- ing the other letters;
S1 that which circularly permutes a1, b1, c1, . . . . Further, let T = (t1, t2, . . . , tµ, . . .) be any group of substitutions which permute the q systems a, b, c, . . . , a1, b1, c1, . . . amongst themselves by replacing corresponding letters with each other.
The substitutions of the group tt derived from S, S1, . . . and from T will all be of the general form tµSαSβ . . .. For let, for example, SβtµSα be one of these substitutions: it is identically equal to tµt−µ 1SβtµSα. Now if we suppose,for instance, that tµ replaces the system a, b, c, . . . by the system a1, b1, c1, . . . ,t−1Sβtµ will be equal to Sβ: the given substitution will thus be equal to tµSβSα,µ 1 1or, as S1 is exchangeable with S, to tµSαSβ. 英国数学代考
The order of tt will be equal to M pq, M being the order of T : indeed, in the general expression of its substitutions tµSαSβ . . ., one may take for tµ any of the M substitutions of T , then assign to each of the exponents α, β, . . . all the possible values inferior to p, and all the substitutions thus obtained will be distinct; for if we had, for example,
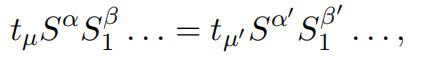
we would deduce
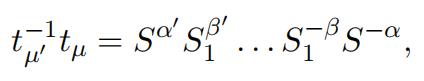
an impossible relation if µj differed from µ, because the substitution in the first term would move the systems, which the second term would not do. So, we’ll have
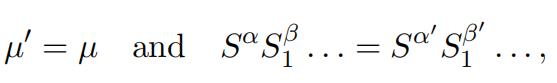
2p. 27f in C. Jordan, Trait´e des substitutions et des ´equations alg´ebriques. Paris, 1870. xviii+667 pages. Translated from the French by Matt & Shuyang.
whence
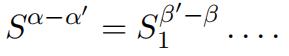
But the substitution in the first term of this last relation moves only the letters in the first system, which the second term leaves unmoved; so they can only be identical if they both reduce to unity; thus α = αj; similarly we’ll have β = βj,
etc. Thus the equality tµSαSβ . . . = tµj Sαj Sβj . . . cannot persist, unless we have,
at once, µ‘ = µ, α‘= α, β‘ = β, . . . . 英国数学代考
With that, let pϕ be the highest power of p contained in the product 1·2·3 · · · q; we can by hypothesis choose T so that its order be equal to p . The order of tt will then be equal to pϕ+q = pf .
Now answer the following. For all parts except d) and p), one line is enough.
a)Which theorem from our course is Lemma II most similarto?
b)What proof technique is Jordanusing?
c)Why is the lemma true for k< p?
d)Why can every k be put in the requiredform?
e)What are the “systems a, b, c, . . . , a1, b1, c1, . . . ”?
f) What kinds of permutations are S, S1,…?
g)Whatdo the elements of T do to the systems?
h)What is G generatedby?
i)Whatdoes Jordan mean by “the substitutions of the group G […] will all be of the general form tµSαSβ . . . ”? Explain in terms of G, T , and the cyclic subgroups generated by S, S1, . . . .
j)Why does 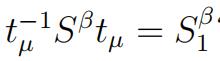 ?
?
k)Whatdoes “S1 is exchangeable with S” mean, and why is it true?
l)What’sthe main result of the penultimate paragraph? 英国数学代考
m)Whyare there p choices for each of the exponents α, β, . . . ?
n)Whatdoes Jordan prove about the groups T and (S, S1, . . .)?
o)Why can we “choose T so that its order be equal topϕ”?
p)Why does ϕ + q = f?
Problem 12. Find and correct 10 mathematical errors from 10 distinct en- tries in the MAT301 Course Glossary. If you list more than 10, we will only grade your first 10.

