Stat 351 Fall 2021
美国统计代写推荐 Suppose that X1, X2, and X3 are independent and identically distributed continuous random variables with common density function f(x).
Assignment 1
Each question is worth 10 marks for a total of 40 marks. Question 5 is a bonus question.
1. 美国统计代写推荐
Let X and Y be independent random variables with X ~U (1,3) and Y~N (0,1).
(a)Determine ,( , ), the joint distribution function of (X, Y)’.
(b)Show directly (by computing the indicated partialderivative) that: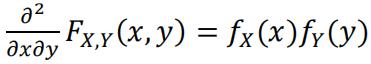
(c)Is this surprising? Why or whynot?
(d)If Z~𝐸𝑥p(4).is independent of X and Y, determine the joint density of (X, Y, Z)’.
2.
Suppose that X~N (0,1). Let Y be independent of X with P(Y = 1) = P(Y = -1) = 1/2. Define the random variable Z be setting Z = XY.
(a)ComputeCov(X,Z).
(b)(Showthat P(Z >= 1) = P(X >= 1). Use this fact to conclude that Z and X are NOT independent. 美国统计代写推荐
(c)Generalizepart (b) to show that P(Z >= x) = P(X >= x) for every . This implies that Z~N (0,1)

3. 美国统计代写推荐
Let (X, Y) be a point that is uniformly distributed on a square whose corners are (±1, ±1). Determine the distribution(s) of the x- and y-coordinates. Are X and Y independent? Are they uncorrelated?{Exercise 1.3. p19}. See example 1.1.
4.
Suppose that X1, X2, and X3 are independent and identically distributed continuous random variables with common density function f(x).
(a)Compute P(X1 >X2)
(b)Compute P(X1 > X2| X1 >X3)
(c)Compute P(X1 > X2| X1 <X2)
Hint: You can answer this problem easily using symmetry.
5.Bonus 美国统计代写推荐
Let (X, Y, Z) be a point chosen uniformly within the three-dimensional unit sphere. Determine the marginal distributions of (X, Y) and X.
{Exercise 1.1. p18}
Finding the marginal distribution of (X, Y)’ involves a computation similar to Example 1.1. However, finding the marginal distribution of just X is much more frustrating.

