Operational Risk and Insurance Analytics
美国统计代写价格 You may use R, Matlab, or any other statistical software of your choice in order to solve some parts of the questions in this assessment.
In Course Assessment:
STAT3022/G022/M022
- This assessment counts for 10% of your fifinal mark for STAT3022/G022/M022.
- You should work in groups of no more than 3 students. You may work on the project alone if you wish, but note that this is not effiffifficient. It is up to you to form your own groups.
- I will request the student ID number of each group member on Tuesday 6th March at the end of the lecture.
- You may use R, Matlab, or any other statistical software of your choice in order to solve some parts of the questions in this assessment.
- Non-submission of this assessment may mean that your overall examination mark is recorded as“non-complete”, i.e., you may not obtain a pass mark for the course.
- The report should be uploaded to Moodle, and offiffifficially ‘submitted’ by 4pm on Thursday, 22nd March.
- Each student must provide a statement of their contribution to the project signed with the submission. 美国统计代写价格
- One member of every group should upload the fifinal version of the report, using the relevant submission link on Moodle (which will appear closer to the deadline), and press ‘submit’. This will require you to read and accept a plagarism statement.
- All remaining members of the group should their press their ‘submit’ button; again this will require each student to read and accept a plagarism statement.
- All groups will be able to see which of their members are yet to press ‘submit’.
- The report won’t be considered submitted until every member has offiffifficially
submitted the report, and this needs to be complete by the deadline above.
- Please note: Each group should submit a single pdf fifile and a single R or Matlab script.
- The R or Matlab script will include your code and comments which may also refer-ence to which question the section of code relates.
- The pdf fifile will consist of your answers to the non-coding parts of the questions and the required output plots.
How will the report be marked? 美国统计代写价格
Your report will be marked out of 100, with 30 percent of the marks allocated for the presentation of the report (including clarity of expression and presentation of proofs, fifigures,plots), and 70 percent of the marks available for the analyses and interpretation.
I will be looking for:
- Clarity of writing the expressions, proofs etc;
(Please remember you Do Not have to type all your report.) 美国统计代写价格
- Ability to select the most important points from an analysis;
- Sensible use and display of plots and tables (if necessary);
- Accuracy of interpretation of results etc.
- Clarity and readability of computer code.
The mark you will receive is your group mark – everyone in the group will be awarded the same mark, except in exceptional circumstances (e.g. a member of a group did not contribute fairly to the project).

1 Compound process models under LDA framework
Question A
(a) Consider a severity model for losses in a given business unit risk type given by
Xi(t) ∼ Gamma(α, β) (1)
Write a closed-form expression for the distribution and density function of the sum of n-losses, considering all Xi ’s are independent and identically distributed random variable with Gamma distribution as mentioned in equation (1). [4]
(b) Write the closed-form expression for the distribution and density function of the compound process LDA model with Poisson frequency with intensity parameter λ and severity model characterised by Gamma distribution, as in equation (1). [4]
(c) Create a Matlab or R script to plot the distribution and density functions of the compound process given by the Poisson-Gamma model, labelling clearly all compo-nents of the plots. Consider a range of parameter values for the LDA model that you may choose, and specify the choices made in the reporting of the result. [8] 美国统计代写价格
(d) Write the steps you would take to simulate the annual loss distribution from this LDA model (Poisson-Gamma) using a Monte Carlo algorithm. [6]
(e) Implement your Monte Carlo algorithm in R or Matlab for 10,000 simulated years for the same range of parameter values for the LDA model (Poisson-Gamma) that you chose previously (specify the choices made in the reporting of the results). Plot histogram estimates of the annual loss distribution and density and compare them to the exact results obtained. [8]
Question B 美国统计代写价格
(a) Consider an α-Stable severity model for losses in a given business unit risk type given by
Xi(t) ∼ Sα(β, γ, δ; 0) (2)
Write a closed-form expression for the distribution and density function of the sum of n-losses when α = 0.5 and β = 1. [4]
(b) Write a closed form expression for the distribution and density function of the compound process LDA model with Poisson frequency with intensity parameter λ and severity model characterised by distribution in equation (2). [4] 美国统计代写价格
(c) Create a Matlab or R script to plot the distribution and density function of the compound process given by the Poisson-Stable model, labelling clearly all components of the plots. Consider a range of parameter values for LDA model that you may choose, and specify the choices made in the reporting of the result. [9]
(d) Write the steps you would take to simulate the annual loss distribution from this LDA model (Poisson-Stable) using a Monte Carlo algorithm. [5]
(e) Implement your Monte Carlo algorithm in R or Matlab for 10,000 simulated years for the same range of parameter values for the LDA model (Poisson-Stable) that you chose previously (specify the choices made in the reporting of the results). Plot histogram estimates of the annual loss distribution and density and compare them to the exact results obtained. [8]
2 Heavy tailed loss models and quantiles
Question A
(a) Provide a detailed defifinition of a generic heavy tailed severity model, with distribution function F that admits a density function f, from the perspective of the properties of the hazard function and hazard rate. Start by defifining the hazard function and hazard rate, then explain its properties and link this to the heavy tailedness of the distribution. Provide a worked example to illustrate this point using one of the one or two parameter family of severity models. [10] 美国统计代写价格
(b) Consider the annual loss random variable Z given by compound process LDA model
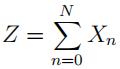 for frequency random variable N ∼ G(n) and independent severity random variables
for frequency random variable N ∼ G(n) and independent severity random variables
that are independent identically distributed according to Xn ∼ F(x) for all losses.
Find an expression for the mean and variance of the annual loss in terms of moments of N and Xn. In the process show that following bound holds
V ar[Z] ≤ E[X 2 ] max(E[N], V ar[N]) (4)
[13]3 Risk measure calculations and asymptotic approximations 美国统计代写价格
Question A
(a) Defifine the VaR measure in a suffiffifficiently general form to deal with difffferent types of supports for the loss random variable. [2]
(b) Provide a defifinition for the Expected shortfall risk measure. [2]
Question B
(a) Consider Poisson-Lognormal LDA model. Provide a fifirst order asymptotic approximation for the tail function of this model. [3]
(b) Consider the fifirst order asymptotic to the tail function derived in part (a). Create an R or Matlab script to plot this function for a range of parameters λ, µ and σ that you choose. [10]

