STA 142A: Homework 1
美国统计代写 But copying of the homework constitutes a violation of the UC Davis Code of Academic Conduct and appropriate action will be taken.
- Homework due in Canvas: 01/29 at 11:59PM.
- Please follow the instruction in canvas regarding HWs.
- You are encouraged to discuss about the problems with your classmates.
But copying of the homework constitutes a violation of the UC Davis Code of Academic Conduct and appropriate action will be taken.
1.Question 4 in page 120 of the textbook. (Note: this is an open endedquestion). 美国统计代写
2.Linear regression simulation. Consider the linear regressionmodel
yi = β0 + β1xi + si, i = 1, . . . , n,
where β0 = 5, β1 = 3 and si ∼ N (0, 1) and xi ∼ Uniform(0, 1).
a)Generate n = 100 data points (xi, yi) from the above model. Plot the data. Fit alinear regression line model using python and add the fitted line to the plot. You could use the LinearRegression() function from Scikit learn See documenta-tion at https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LinearRegression.html
b)Repeat the experiment in part (a) for 1000 times (without plotting). Note that you willgetdifferent estimates of β1. Denote them as βˆ(1), βˆ(2), . . . , βˆ(1000). What is the mean of these values ? Plot a histogram of βˆ(1), βˆ(2), . . . , βˆ(1000). 美国统计代写
c)Repeat (b) but now with sibeing a standard Cauchy How does the histogram change ? Specifically, comment about the tails of histogram. (Note: Here, you are still using least-squares linear regression. Only the data generating process is changed.)
3.Question 6 in page 170 of the textbook. 美国统计代写
4.Bayes Classifter-I. Suppose that Y ∈ {0, 1} and P(Y = 1) = 1/The distribution of
X|Y = 0 is discrete and is specified by
P (X = 1|Y = 0) = 1/3 P (X = 2|Y = 0) = 2/3.
The distribution of X|Y = 1 is discrete and is given by
P (X = 2|Y = 1) = 1/3 P (X = 3|Y = 1) = 2/3. 美国统计代写
Find the Bayes Classifier (also called as Bayes optimal classification rule).
- Bayes Classifter-II Let X ∈ R correspond to input data and Y ∈ {+1, −1} correspond to binary labels. Suppose we assume the following model for the conditional probabilityof Y = 1 given X = x
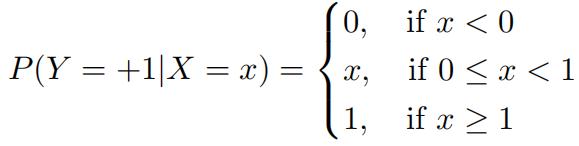
Let f be a classifier and consider the loss function defined as follows:
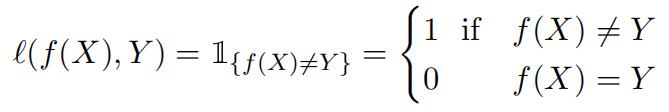
What is the decision boundary (value of x) that minimizes the risk? Now suppose we assume the following model for the conditional probability of Y = 1 given X = x
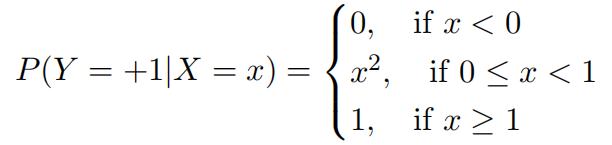
What is the decision boundary (value of x) that minimizes the risk?

更多代写:新西兰CS代写 新加坡Cs代考 新西兰Essay代写 信息技术Essay代写 信息技术论文代写 国际商务论文代写
