School of Mathematics and Statistics
MT4516 Finite Mathematics
美国数学作业代写 Prove that there are no self-orthogonal Latin squares of order 3; fifind a self orthogonal Latin square of order 4.
1.(i) Find a family of three subsets of {1, 2, 3} with exactly three SDRs.
(ii) Find a family of four subsets of {1, 2, 3, 4} with exactly two SDRs. Justify your answer.
2.Prove that there is no Latin square orthogonal to the square
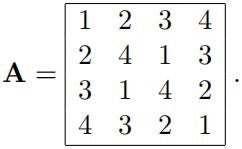
3.A transversal in a Latin square L of order n is a set of n entries of L, one from each row and each column, such that no two entries contain the same symbol. 美国数学作业代写
(i) Let A be the following Latin square.
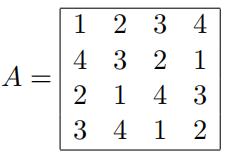
Exhibit a set of 4 disjoint transversals of A.

(ii) Let B be the following Latin square.
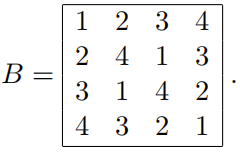
By considering the existence of a transversal containing the (1, 1)th entry of B, prove that it is not possible to fifind a set of 4 disjoint transversals of B.
(iii) Prove that a Latin square L of order n has an orthogonal mate if and only if L has n disjoint transversals.
4.Let GF(4) be the fifinite fifield with four elements (see the lecture notes).Use GF(4) to construct three mutually orthogonal Latin squares of order4.
5.Construct two orthogonal Latin squares of order 12. (Hint: Use direct products.) 美国数学作业代写
6.A Latin square is said to be self-orthogonal if it is orthogonal to its own transpose.
(i) Prove that if A = (aij)n×n is a self-orthogonal Latin square then all the entries aii, 1 ≤ i ≤ n, are distinct.
(ii) Prove that there are no self-orthogonal Latin squares of order 3; fifind a self orthogonal Latin square of order 4. 美国数学作业代写
(iii) Prove that the direct product of two self-orthogonal Latin squares is again a self-orthogonal Latin square. (Hint: You may use (A × B) T = AT × BT).
(iv) Let n > 3 be a prime power, and let F = {f1,f2, . . . ,fn} be the fifinite fifield with n elements. For an arbitrary t ∈ F, with t ≠0, 1 andt + t ≠1, defifine an array At = (aij)n×n by a(t)ij= tfi + (1 − t)fj . Prove that At is a self orthogonal Latin square.

