School of Mathematics and Statistics
MT4003 Groups
Problem Sheet II: Subgroups
美国数学作业代做 Show that H is a subgroup of S4. Construct the Cayley table of H. Is H isomorphic to a group we have already seen?
1.Consider H = {1, (1 2)(3 4), (1 3)(2 4), (1 4)(2 3)}.
Show that H is a subgroup of S4. Construct the Cayley table of H. Is H isomorphic to a group we have already seen?
2.Let n > 1. Show that H = { σ ∈ Sn | nσ = n } is a subgroup of Sn isomorphic to Sn−1.
[Hint: Defifine a suitable isomorphism Sn−1 → H. Also note in the above formula, nσ denotes the image of n under the permutation σ.]
3.Let G be an abelian group and let H be a subgroup of G. Show that H is also abelian.
4.Let G be a group and let H be a subset of G. Show that H is a subgroup of G if and only if H is a non-empty subset of G such that xy−1 ∈ H whenever x, y ∈ H.
5.Let G be a group and let H and K be subgroups of G. Prove that the union H∪ K is a subgroup of G if and only if either H ⊆ K or K ⊆ H. 美国数学作业代做
6.Let a and b be elements of a group that commute (that is, such that ab = ba). Show that
o(ab) 6 lcm(o(a), o(b)).
Deduce that the set of all elements of fifinite order in an abelian group is a subgroup. [This is called the torsion subgroup.]
Is the same true for the set of elements of fifinite order in an arbitrary group?
7.Let n be a positive integer. Let
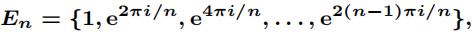
the set of all complex numbers z satisfying zn = 1.
(a) Show that En forms a group under multiplication.
(b) Is En abelian?
(c) Let g = ![]() Show that En = 〈g〉.
Show that En = 〈g〉.

8.Let σ = (1 4)(2 6) and τ = (2 5)(3 6). Find all elements in the subgroup 〈σ,τ〉, τ of S6.
9.Let n be a positive integer with n ≥ 3. Let ∆ denote the regular polygon with n sides. A symmetry of ∆ is an invertible transformation that maps vertices to vertices and edges to edges.
(a) How many symmetries of ∆ are there? How many of these are rotations and how many are reflflections?
(b) Is it true that the composition of two symmetries is again a symmetry of ∆? 美国数学作业代做
(c) Show that the set G of all symmetries of ∆ forms a group under composition.
Label the vertices of ∆ clockwise 1, 2, . . . , n and set X = {1, 2,…,n}. For each g ∈ G, defifine a map Øg : X → X by:
kØg is the label ![]() such that g maps the vertex labelled k to the vertex labelled
such that g maps the vertex labelled k to the vertex labelled ![]() .
.
(d) Show that φg is a permutation of X for every g ∈ G.
(e) Let a denote the rotation of ∆ clockwise through an angle of 2π/n and let b denote the reflflection of ∆ in the axis that passes through the vertex 1. Calculate Øa and Øb.
(f) Show that g → Øg group of order 2 is an isomorphism G → D2n from the symmetry group of ∆ to the dihedral 2n.
10.(a) Find the order of the symmetric group Sn of degree n. 美国数学作业代做
(b) Show that the alternating group An has index 2 in Sn and hence determine its order.
11.Consider the symmetric group S4 of degree 4. For each divisor m of its order, fifind a subgroup of S4 of order m.
12.For each of the following subgroups H of S4, determine its index in S4. Also fifind a system of representatives for the right cosets in S4; that is, fifind a subset T = {t1, t2,…,tk} of S4 such that the distinct right cosets of H in S4 are Ht1, Ht2, …, Htk:
(a) H = {1, (1 2)(3 4), (1 3)(2 4), (1 4)(2 3)};
(b) H = S3;
(c) H = D8.
13.(a) List the elements of the dihedral group of order 8 and determine the order of each element. 美国数学作业代做
Is this dihedral group isomorphic to C8? Is it isomorphic to the quaternion group Q8?
Let H be the subgroup generated by {(1 2)(3 4)}. List the left and right cosets of H in D8
(b) Is the dihedral group D12 of order 12 isomorphic to A4?
(c) Is the dihedral group D24 isomorphic to S4? 美国数学作业代做
14.Let G be a group and let H be a subgroup of G. Show that two left cosets xH and yH (where x, y ∈ G) are equal if and only ifx−1y ∈ H.
15.Let G be a group and H and K be subgroups of G. Let CH, CK and CH∩K denote the set of right cosets in G of H, K and H ∩ K, respectively. Defifine a mapping α: CH∩K →CH × CK by
((H ∩ K)x ) α= (Hx, Kx).
Prove that ↵ is well-defifined and one-one.
Deduce that
|G : H ∩K| ≤ |G : H|·|G : K|.
Deduce that the intersection of two subgroups of G of fifinite index is also a subgroup of fifinite index.

更多代写:微积分网课代修 线上考试作弊方法 温哥华网课代上 新加坡eduessay代写 物理学paper代写 数学math代写
