STAT GR5241 – Take Home Problem [20 pts]
编程语言作业代写 Recall: problem 1 from in-class fifinal exam Consider flflipping a biased coin several times until a head appears.
- Include a brief written summary of your results as a .html or .pdf.
- Also include a complementary code fifile.
- You can choose any programming language to solve this problem.
- The dataset of interest is GoemMixture.csv.
Recall: problem 1 from in-class fifinal exam 编程语言作业代写
Consider flflipping a biased coin several times until a head appears. Defifine the geometric random vari-able:
X = “number of trials until the fifirst success (inclusive)”
In our case X represents the number of coin flflips until the fifirst heads and has probability mass function:
f(x|p) = p(1 − p)x–1 , x = 1, 2, . . . ,
where p = P(H) is the success probability of landing a heads.
Now consider an urn of K > 0 coins, each having its own success probability p1, p2, . . . , pK. Further, suppose that you randomly draw one of the K coins from the urn and flflip that same coin until a head appears. Once you have recorded the number of trials that it took to show your fifirst success, you replace the coin back into the urn and repeat the experiment numerous times. This new random variable X is now drawn from a mixture of geometric distributions:
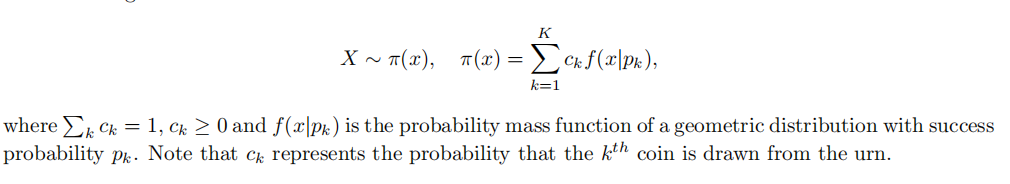
Solve the following problem (in-class exam)
Suppose that after observing n draws from the above mixture distribution, you would like to identify which cases came from each coin. Write down the EM algorithm for estimating parameters c1, c2, . . . , cK and p1, p2, . . . , pK.
Hint: The expected value of the geometric random variable is 1/p, where p is the success probability.
Take home problem (required problem) 编程语言作业代写
Manually code the EM algorithm based on problem 1 from the in-class fifinal exam. Your goal is to cluster each case in the dataset GoemMixture.csv, assuming a mixture of geometric distributions. Some notes follow:
- Choose K = 3 clusters.
- Make sure to try several randomized initial values and pick the fifinal cluster assignment with the highest likelihood.
- Your EM algorithm should break based on the convergence criteria
‖A(j+1) − A(j) ‖ < δ,
for some δ > 0. Note that ‖·‖ is the matrix 1-norm (the largest sum of column absolute values).
- Choose some small δ > 0 in your solution.
- Include some graphic of your choice that displays the fifinal cluster assignments.

其他代写: homework代写 java代写 matlab代写 python代写 report代写 paper代写 assignment代写 finance代写 program代写 project代写 essay作业代写 作业代写 作业加急 英国代写 北美作业代写 加拿大代写
合作平台:essay代写 论文代写 写手招聘 英国留学生代写
代写.png)
