CMPT 225
Fall 2020
T.Shermer
编程考试助攻代写 Final Exam:2 hours and 50 minutes for solving the problems, then 20 minutes to scan/prepare a PDF and upload it to CourSys.
Final Exam
2 hours and 50 minutes for solving the problems, then 20 minutes to scan/prepare a PDF and upload it to CourSys. No web searching or surfing. Open book. You must submit your own work under your own name. 10 questions.
Question 1. (8%; 2% each)
In each of the following, an ADT name is followed by three data structures. Which of the three data structures is the better (or more usual) choice for implementing the ADT?
a. Stack: tree, array, skiplist
b. Priority Queue: hash table, heap, 2-3-4tree
c. Ordered Map: hash table, heap, skiplist
d. Map: hash table, array, binary searchtree
Question 2. (10%; 5% each) 编程考试助攻代写
a. Write pseudocode for a recursive function that finds the maximum of an array of integers without using any
b. Describe a method for finding both the minimum and maximum of n numbers using at most 3n/2 comparisons. You may not use a sorting or selection algorithm. (Hint: first construct a group of candidate minimums and a group of candidatemaximums)
Question 3. (10%)
Give pseudocode for a postorder traversal of a Binary Search Tree, where the computation at each node is to print the node’s data, indented (2 times the depth of the node in the tree) spaces.
Question 4. (12%) 编程考试助攻代写
Describe the Queue ADT. Include an example Applications Programmer Interface (API). (But don’t give just the API – state what it does.)
Question 5. (12%)
In union-find, suppose we have n elements and each element is an object that has its data and a pointer to a set. The set objects contain a name and a list of elements in the set. Each element starts in its own set. When two sets are unioned, the set retained for the union is the larger of the two sets. Asymptotically, how much time does it take to perform n unions? Why?
Question 6. (8%) 编程考试助攻代写
Describe the information that is stored at an internal node of an AVL tree.
Question 7. (10%)
Bill claims that a preorder traversal of a min-heap will list its keys in nondecreasing order. Show an example of a heap that proves him wrong.
Question 8. (10%; 2% each) 编程考试助攻代写
Define the following terms precisely.
a. The load factor of a hash
b. A descendent of a node in a
c. An Adapter
d. The Heap Property in a
e. The Greedymethod.
Question 9. (10%)
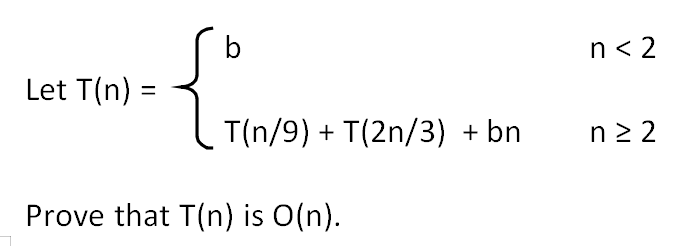
Question 10. (10%) 编程考试助攻代写
Analyze the worst-case time complexity of Jumble(A) in the following pseudocode, when A is an array with n elements. Do not try to figure out what the code does; just consider its running time. Show your work.
jumble(A) {
return jumble(A, 0, A.size)
}
jumble(A, j, k) {
If (k – j) < 3 then return;
n = (k+1) – j.
jumble(A, j, j + n/4)
jumble(A, j + 3n/4, k)
for k = 1 to n/4 {
min = min(A[j + k], A[j + n/4 + k ]);
max = max(A[j + k], A[j + n/4 + k]);
A[j + k] = min;
A[j + n/4 + k] = max;
}
If A[j + n/2 – 1] < A[j+n/2] then {
jumble(A, j + n/4, j + n/2)
jumble(A, j + n/2, j + 3n/4)
for k = 1 to n/4 {
min = min(A[ j+ n/2 + k], A[j + 3n/4 + k]);
max = max(A[j + n/2 + k], A[j + 3n/4 + k]);
A[j + n/2 + k] = min;
A[j + 3n/4 + k] = max;
}
}
}

其他代写:考试助攻 program代写 essay代写 web代写 cs作业代写 加拿大代写 北美代写 北美作业代写 数据分析代写 澳大利亚代写 英国代写 homework代写 web代写 finance代写 Exercise代写
